안녕하세요 jiogenes 입니다.

오늘은 허깅페이스의 peft 라이브러리에서 지원하는 대표적인 PEFT 방법 중 하나인 LoRA와 LoRA의 개선작들에 대해 알아보겠습니다. 논문 자체에 대한 리뷰 보다는 논문에 나와있는 메소드 위주로 알아보고 어떤 차이점이 있는지 알아보도록 하겠습니다.

PEFT란?

우리가 흔히 말하는 LLM은 Large Language Model의 약자로써 말그대로 거대한 언어 모델입니다. 언어 모델이란 이전 단어의 순열을 보고 다음 단어가 뭐가 나올지 잘 맞추는 모델을 말합니다. 우리 인간은 모두 뇌속에 초거대 언어 모델을 하나씩 가지고 있는 셈이지요. 하지만 이렇게 다음 단어가 어떤게 나올지 예측하는 것 만으로는 실생활에 사용하기 힘듭니다. 왜냐하면 우리는 인공지능 모델에게 어떠한 명령을 내렸을때 그에대한 적절한 답을 받기를 원하는데, 언어 모델만으로는 우리의 명령 뒤에 이어 붙일 말만 지어내기만 하고 상황, 문맥상 우리가 원하는 답을 얻기가 매우 어렵습니다. 흔히 알고있는 GTP, BLOOM, Mistral, Falcon, Llama 등등이 대표적인 순수한 언어 모델 입니다.

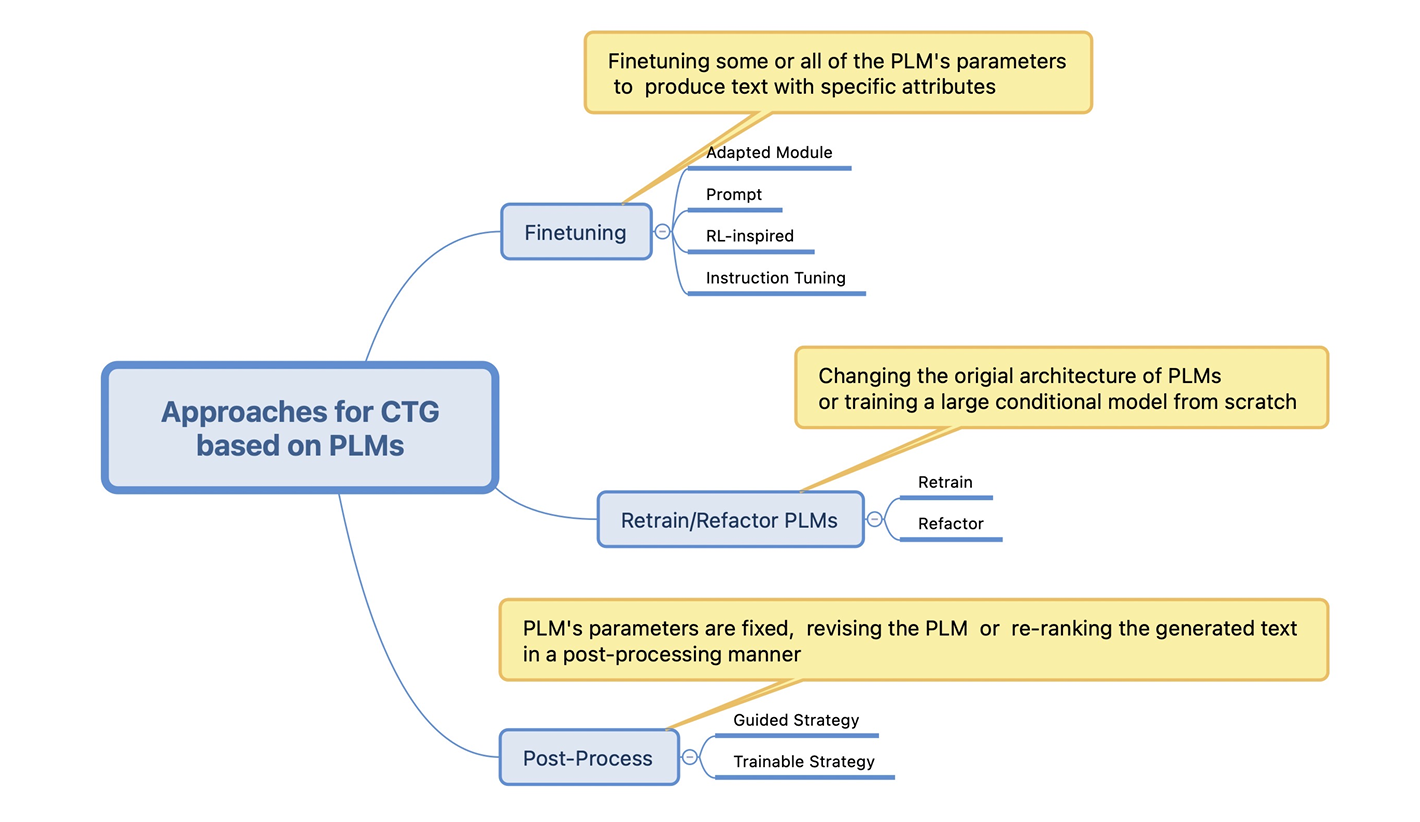
그림1. CTG 구분

때문에 연구자들은 언어에 대한 사전지식이 있는 학습된 LLM을 명령어와 그에 대한 적절한 대답이 있는 데이터를 통해 실생활에 활용할 만한 언어 모델을 만들고자 하였습니다. 이렇게 생성되는 텍스트를 조절하는 방법에 대한 연구분야가 바로 CTG(Controllable Text Generation)입니다. CTG 서베이 논문에 의하면 CTG는 그림1 과 같이 구분이 가능한데, 오늘 우리가 알아볼 방법은 Finetuning 방법 중 하나입니다.

다양한 chatting 및 instruction-following 데이터셋으로 파인튜닝 된 모델들이 현재 우리가 쓰고있는 chatGPT와 더불어 Bard, Llama2 chat, Vicuna, Guanaco, alpaca, GPT4ALL 등등입니다. 또한, 학습되는 데이터에 따라 소스 코드만 알려주는 모델, 힘이나고 좋은 말만 해주는 모델, 나쁜 말만 하는 모델 등 다양한 모델을 파인튜닝을 통해 만들어 낼 수 있게 되었습니다.

하지만 이런 거대 모델들은 기본 적으로 파라미터가 60B를 가뿐히 넘기 때문에 Finetuning을 조금만 할려고 해도 웬만한 GPU로는 어림도 없습니다. 간단한 예시를 들어보자면, 모델을 full fine-tuning하려면 weight, optimizer states, gradients, input data등의 메모리가 요구되므로 통상적으로 모델 가중치의 2~3배의 메모리가 요구됩니다. 따라서 60B 모델을 full fine-tuning하기 위해서는 60B * 4(Bytes) * 3 = 약 700GB의 메모리가 요구됩니다. 700GB의 GPU 메모리라니 정말 무시무시합니다 😱

PEFT는 Parameter Efficient Fine-Tuning의 약자로써 이런 거대한 Pre-trained 모델을 fine-tuning 할 때 모든 파라미터를 업데이트 하지 않고 일부 또는 소수의 파라미터만 업데이트 하는 방식입니다.

그림2. CTG 방법 중 Fine-tuning에서 특별히 파라미터를 적게 사용하는 방법을 PEFT라고 한다.

PEFT 기법은 이미 이전에도 많이 연구 되어 왔지만 PEFT 라는 용어는 2022년을 전후로 사용한것 같습니다. (당시 논문들을 살펴보고 난 후의 제 뇌피셜입니다^^) 그리고 2023년 초에 허깅페이스에서 peft라는 파이썬 라이브러리를 배포하면서 사람들에게 널리 알려지게 되었습니다.

Previous

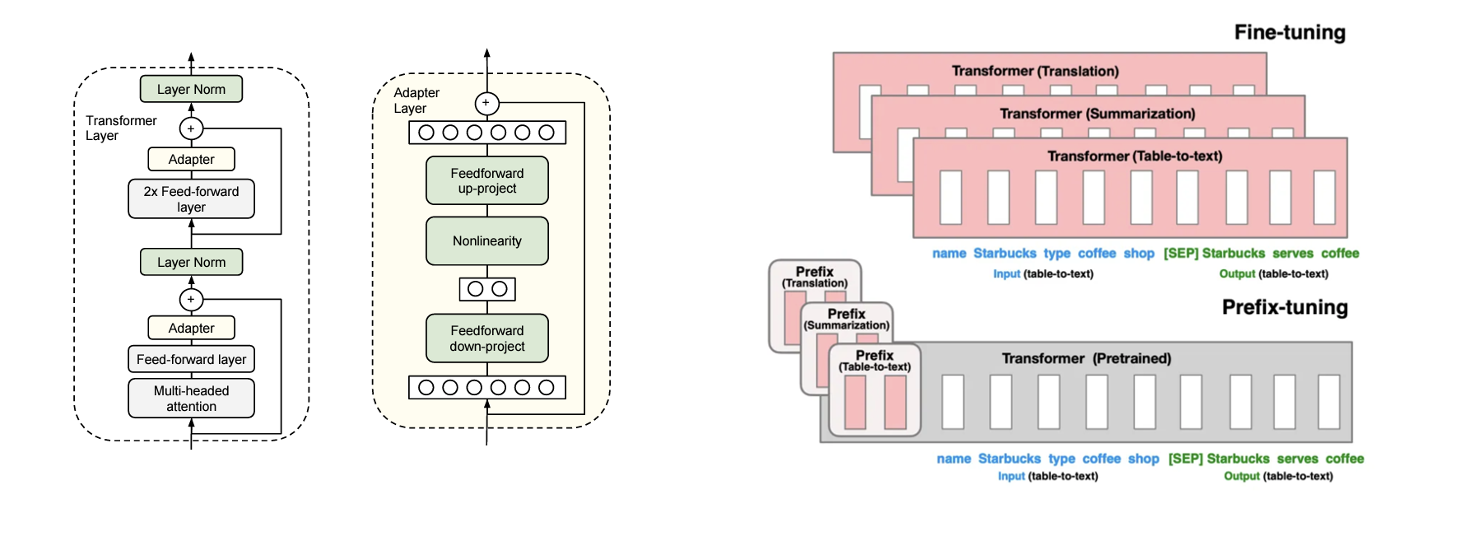
그림3. Adapter와 Prefix tuning

LoRA 이전의 대표적인 PEFT 방법은 Adapter와 Prefix-tuning과 같은 방법들이 있었습니다. 하지만 Adapter는 transformer 모델의 중간에 삽입되는 형태라서 네트워크 깊이 자체가 깊어지는 형태였습니다. 따라서 네트워크 깊이에 따른 inference latency가 발생합니다. 네트워크 깊이가 깊어질수록 학습 속도는 물론 추론 속도 또한 더 오래 걸리겠죠. 또, prefix tuning은 입력 시퀀스의 일부를 할애해서 추가학습 하는 형태이기 때문에 학습 자체가 어렵고 그만큼 입력 시퀀스 길이가 짧아지는 단점이 있습니다. 이로인해 더 많은 prefix를 붙일수록 오히려 성능이 감소하는 현상이 나타나게 됩니다.

LoRA

LoRA는 2021년 마이크로소프트에서 발표한 논문이며 아카이브에만 올라와있습니다. 논문에서 GPT3에 대한 실험을 진행했기 때문에 openAI의 지분이 있는 마이크로소프트에서만 실험을 진행할 수 있었을 것입니다. 그래서 다른 학회나 저널에 올리지 않고 아카이브에만 올린것이 아닌가 추측해 봅니다.

LoRA의 동기는 위에서 설명했듯이 거대 모델을 부분 파인튜닝 하기 위한 방법을 개발하는 것 입니다.

LoRA를 이해하기 위해서는 Low-rank approximation(decomposition)에 대해서만 알고 계시면 됩니다. (추천 시스템에서는 Matix factorization이라고도 합니다)

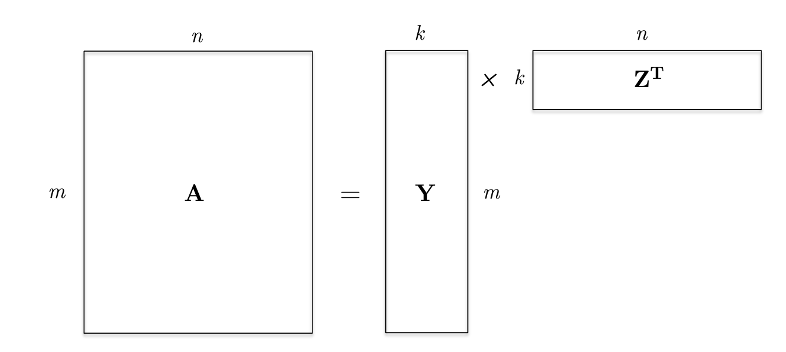
그림4. Low-rank Matrix Approximation (출처 CS168)

위 그림과 같이 $A$ 행렬을 더 작은 rank를 가진 두 개의 행렬 $Y\in\mathbb{R}^{m\times k},Z\in\mathbb{R}^{n\times k}$ 의 곱으로 근사하는 것을 Low-rank approximation 이라고 합니다.

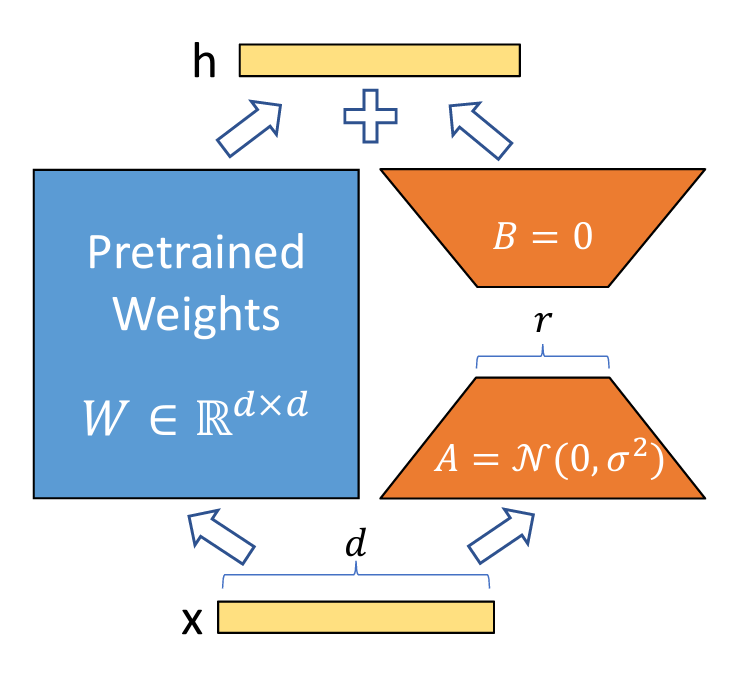
그림5. LoRA

LoRA는 위 그림과 같이 원래 가중치 행렬(Query, Key, Value, Embedding, Feed Foward 등)을 다른 두 개의 행렬의 곱으로 근사합니다. 간단한 예시를 들어보자면, 원래 가중치 행렬의 크기가 (1024, 1024) 라고 한다면 업데이트 할 총 파라미터의 수는 1,048,576개 입니다. 하지만 이를 rank 1짜리 LoRA 행렬을 이용하면 (1024, 1) 행렬 2개로 근사가 가능하므로 업데이트 할 파라미터 수는 2,048개 뿐입니다. (업데이트 할 파라미터가 512배가 줄어들었습니다!) rank가 작을수록 메모리 절감 효과가 커지겠지만 적절한 성능을 위해서 자신의 테스크에 맞는 적당한 rank수를 찾아야 합니다.

가중치 행렬에 들어오는 입력을 $x$, 가중치 행렬을 통해 나오는 hidden state를 $h$, 업데이트를 하지 않을 (pre-train되고 freezing시킨) 행렬을 $W_0$, 업데이트 할 가중치 행렬을 $\Delta W=BA$라고 할 때, LoRA를 수식으로 나타내면 다음과 같습니다.

\[h=W_0 x + \Delta Wx=W_0 x+BAx\]

$W_0$는 쿼리, 키, 벨류, 임베딩, 피드포워드 ($W_q,W_k,W_v,W_o,W_{ff}$) 중의 한 행렬입니다.

이렇게 LoRA는 행렬 근사 방법을 통해 입력 데이터를 parallel하게 계산할 수 있으므로 학습과 추론에서 latency가 사라지게 됩니다.

LoHa

LoHa는 순수하게 PEFT 방법을 위해서가 아니라 federated learning(연합학습, FL)을 위한 거대 모델 근사 방법에 대한 논문입니다. 하지만 huggingface peft 라이브러리에서는 연합학습 보다는 PEFT 방법론 자체에 초점을 맞춰 LoRA보다 더 효율적인 방법이라 소개하고 있습니다. 논문에서는 연합학습에 대한 백그라운드와 연합학습에 관련된 실험들이 나오기 때문에 저도 PEFT 방법론에만 초점을 맞춰 글을 써보겠습니다.

LoHa는 한마디로 가중치 행렬 근사를 Hadamar Product(아다마르 곱)를 통해 근사한 것입니다. Hadamar Product는 element-wise product와 똑같습니다.

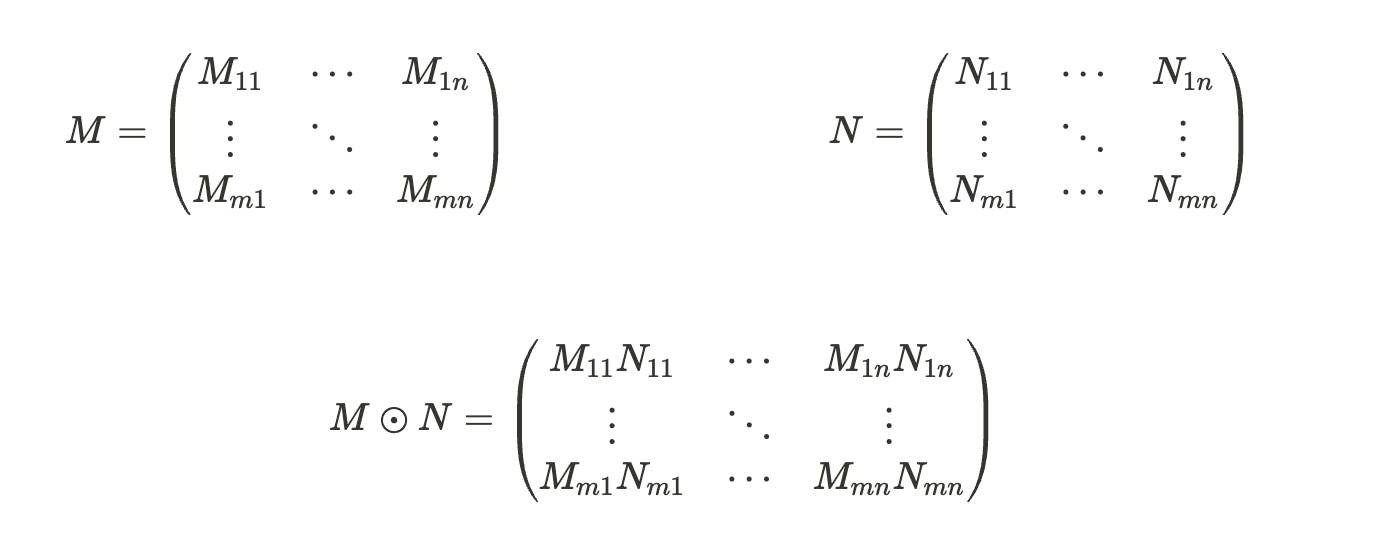
Untitled

LoHa는 행렬의 element-wise 곱을 통해 어떻게 원래 가중치 행렬의 rank를 보존할 수 있는지 수학적으로 증명을 했습니다.

명제1. $X_1\in \mathbb{R}^{(m×r_1)}, X_2\in \mathbb{R}^{(m×r_2)}, Y_1\in \mathbb{R}^{(n×r_1)}, Y_2\in \mathbb{R}^{(n×r_2)}$ 이고 $r_1,r_2 \le min(m,n)$일 때, $W=(X_1 Y_1^T)\odot (X_2 Y_2^T) \in \mathbb{R}^{m\times n}$ 에 대해, $rank(W) \le r_1 r_2$ 이다.

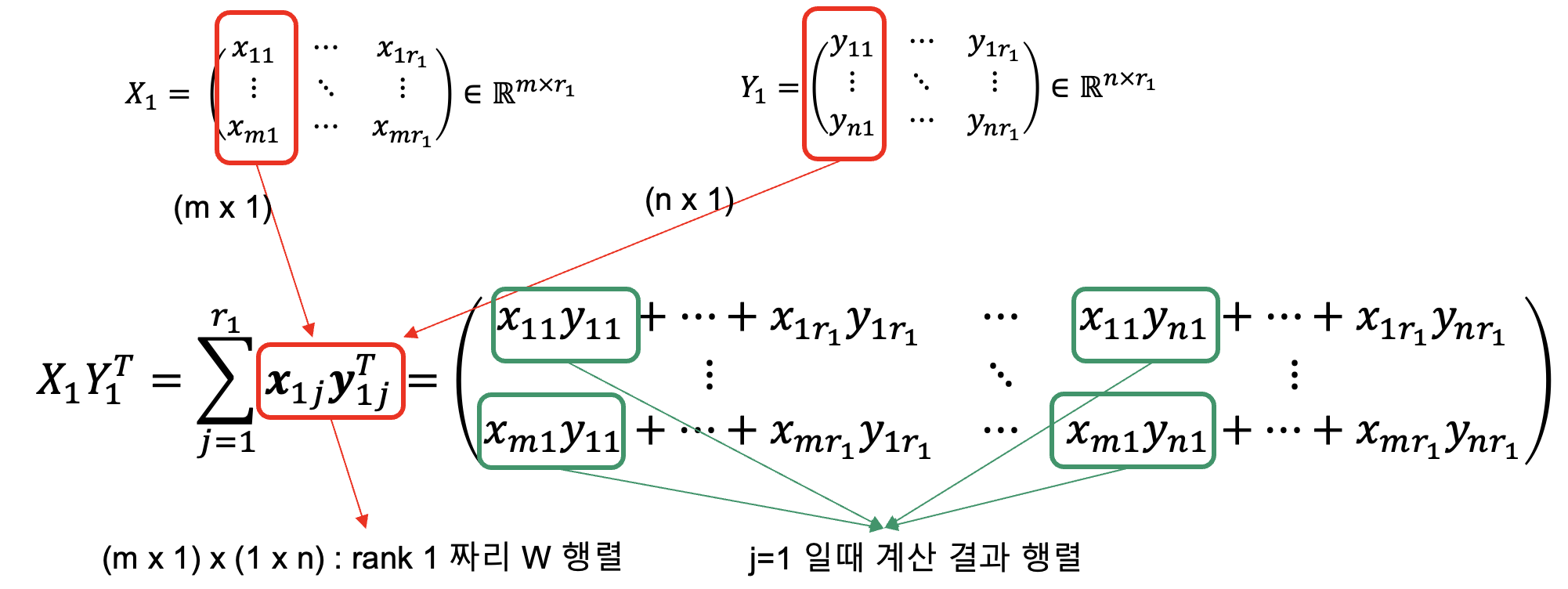
증명1. $X_iY_i^T$는 $j$번째 열벡터의 곱인 $x_{ij}y_{ij}^T$ ($x_{ij} \in \mathbb{R}^{m\times 1}, y_{ij} \in \mathbb{R}^{n\times 1}$)로 rank 1짜리 행렬의 합으로 분해가 가능하다. 따라서 근사한 행렬 $X_iY_i^T=\sum_{j=1}^{j=r_i}x_{ij}y_{ij}^T$ 와 같이 나타낼 수 있다. 따라서 다음과 같은 식이 성립한다.

\[W=(X_1 Y_1^T)\odot (X_2 Y_2^T)=\sum_{j=1}^{r_1}x_{1j}y_{1j}^T \odot \sum_{j=1}^{r_2}x_{2j}y_{2j}^T=\sum_{j=1}^{r_1}\sum_{j=1}^{r_2}(x_{1j}y_{1j}^T)\odot(x_{2j}y_{2j}^T)\]

이 때, $W$는 $r_1 \times r_2$ 갯수 만큼의 행렬로 분해가 가능하므로 $rank(W) \le r_1 r_2$ 이다.

Untitled

명제2. 어떤 정수 $R\in\mathbb{N}$ 이 주어진다면, 다음 조건을 만족하는 최적해는 $r_1=r_2=R$ 이고 최적값은 $2R(m+n)$ 이다.

\[argmin_{r_1,r_2\in\mathbb{N}}(r_1+r_2)(m+n)\quad s.t.\quad r_1r_2\ge R^2\]

증명2. 주어진 조건과 산술-기하 평균 부등식을 이용하면 다음 식이 성립한다.

\[(r_1+r_2)(m+n)\ge2\sqrt{r_1r_2}(m+n)\ge2R(m+n)\]

이 때, $r_1=r_2=R$ 일 때만 등식이 성립한다.

LoHa의 hidden state는 다음과 같이 나타낼 수 있습니다.

\[h=W_0 x + \Delta Wx=W_0 x+(X_1Y_1^T)\odot (X_2Y_2^T)x\]

그리고 위의 증명을 토대로 LoHa는 LoRA의 최대 rank수 $2R$ 에 비해 최대 $R^2$ 만큼의 rank를 가질 수 있게 됩니다.

Untitled

논문을 읽어보면 LoHa는 연합학습에 사용하기 위해 고안되었기 때문에 언어모델 뿐만 아니라 비전처리를 위한 컨볼루션 네트워크 가중치 행렬에 대한 증명도 존재합니다. 이 포스팅은 언어모델을 위한 PEFT에 대한 글이므로 궁금하신 분들은 LoHA논문을 참조해 주세요.

LoKr

마지막으로 LoKr는 예상하시겠지만 가중치 행렬을 다른 알고리즘으로 근사하는 LoRA의 변형 중 하나입니다. LoHa와 달리 LoKr은 Kronecker product(크로네커 곱)를 통해 가중치 행렬을 근사합니다. 그러면 크로네커 곱이 뭔지만 알면 끝나겠죠?

$A\in\mathbb{R}^{a_1\times a_2} , B\in\mathbb{R}^{b_1\times b_2}$ 일때 크로네커곱 $A\otimes B$는 다음과 같습니다.

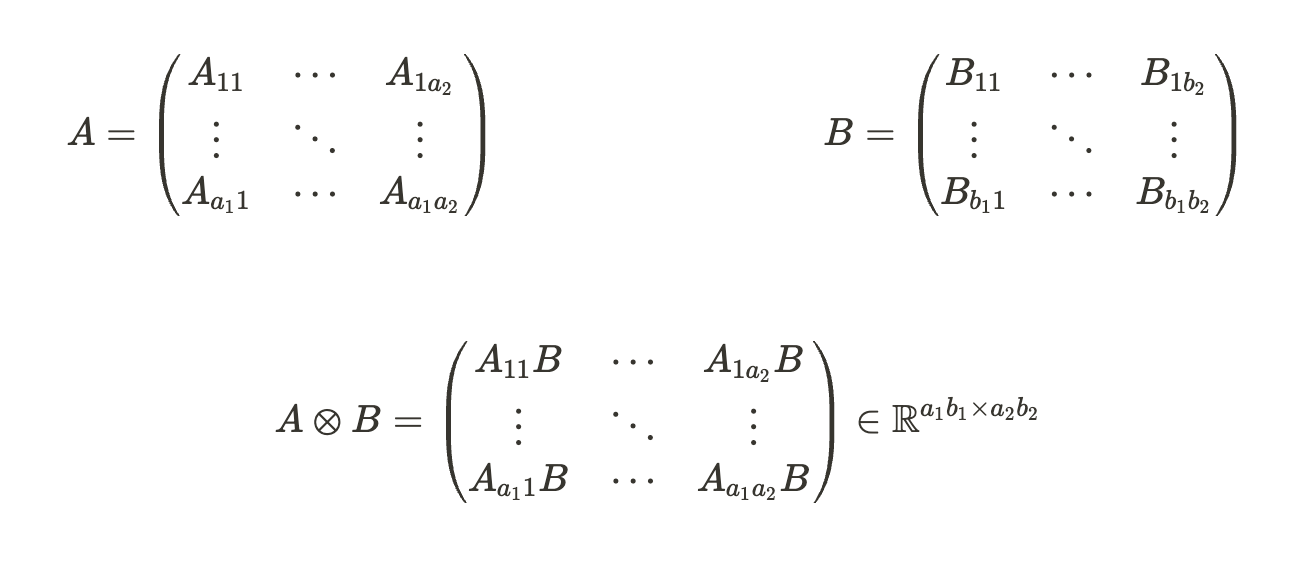
Untitled

행렬 $A, B$가 각각 다른 크기를 가질 때 크로네커 곱 $A\otimes B$는 마치 행렬 $B$가 Weight처럼, 행렬 $A$의 원소 각각이 가중치 처럼 작용합니다. 그리고 결과는 행렬을 다시 행렬처럼 쌓은 형태의 행렬이 만들어집니다.

따라서 크로네커 곱을 사용하면 다음과 같이 LoRA와 rank수는 같지만 파라미터 수를 훨씬 줄일 수 있게 됩니다.

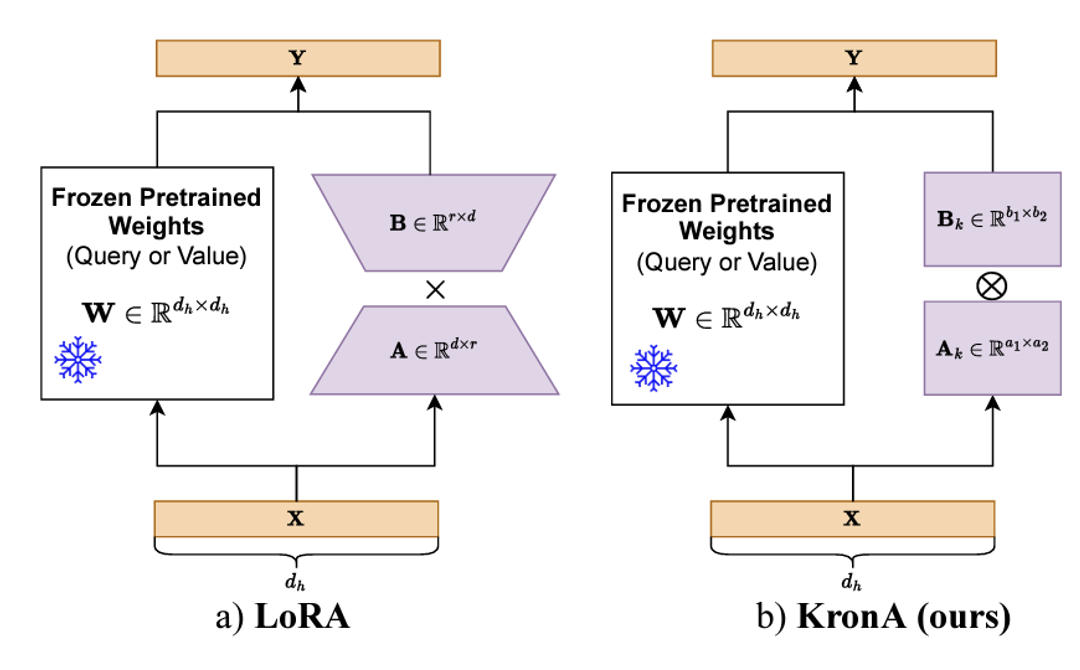
Untitled

크로네커 곱으로 모델 사이즈를 줄일 수 있다는 수학적 증명과 이를 구현한 논문들은 이미 있었지만 크로네커 곱을 LoRA방법론에 사용한 것은 이 논문이 처음입니다. 이렇게 좋은 논문을 쓰기 위해서는 수학 공부도 열심히 해야 되겠네요…😅

마지막으로 LoRA와 LoHa 그리고 LoKr을 비교한 이미지와 표를 보면서 마무리 하도록 하겠습니다.

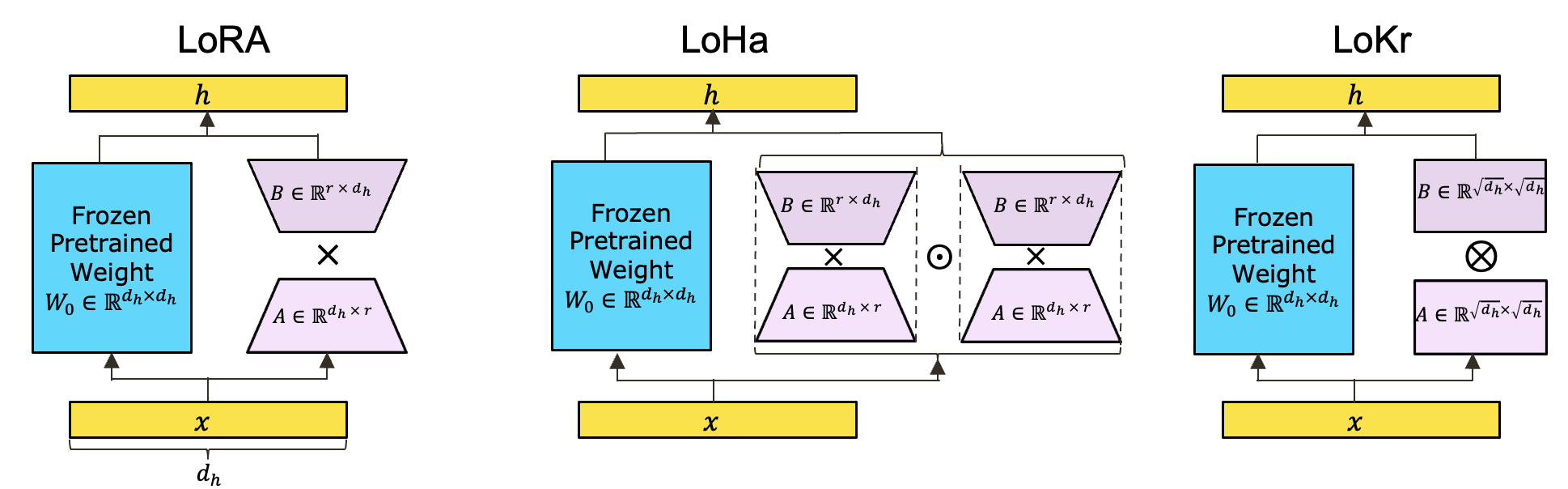
Untitled

  LoRA LoHa LoKr
num of params $r(d_h+d_h)=2rd_h$ $2r(d_h+d_h)=4rd_h$ $2(\sqrt{d_h}\times\sqrt{d_h})=2d_h$
max rank $r$ $r^2$ $r$

결론

이번시간에는 허깅페이스 peft 라이브러리의 LoRA와 그 후속작들을 살펴봤습니다. LoRA의 간단하지만 핵심을 찌르는 아이디어로 인해 현존하는 거대 모델들을 적은 비용으로 파인튜닝할 수 있게 되었습니다. 그리고 이러한 LoRA를 개선하기 위해 많은 수학적, 경험적 아이디어들이 쏟아져 나오고 있습니다. 인공지능을 더욱더 잘 활용하기 위해서는 필수적으로 pre-trained 모델을 목적에 맞게 조금씩 파인튜닝해야 할 것이고 따라서 이러한 PEFT 기법은 모든 AI 엔지니어나 연구원들이 반드시 알아야 하는 필수적인 기법이 될 것입니다. LoRA, LoHa, LoKr은 그 중 가장 대표적인 방법들이고 어떤 원리로 파라미터 효율적인 파인튜닝을 가능하게 했는지 알아보았습니다. 저를 비롯한 이 글을 보시는 모든 분들이 이런 방법을 잘 활용해서 다양한 LLM을 만들고, 또다른 아이디어로 멋진 연구 결과가 나왔으면 좋겠습니다.

봐주셔서 감사합니다 ☺️

잘못된 점에 대한 피드백은 언제나 환영입니다!

참고자료