[논문리뷰] AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning
안녕하세요 jiogenes입니다.
오늘은 대표적인 PEFT 방법 중 LoRA를 개선한 AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning 라는 논문을 리뷰해 보도록 하겠습니다.
혹시라도 LoRA를 모르거나 궁금하신 분들은 이전 포스팅을 참고해 주세요 🤗
소개
이 논문은 2023 ICLR에 출판되었고 제가 포스팅을 하는 시점에 109회가 인용될 정도로 퀄리티가 높고 인기 좋은 논문입니다. 허깅페이스의 peft 라이브러리 중에 가장 먼저 탑 컨퍼런스에 출판된 논문이기도 합니다. 그리고 이것이 논문의 아이디어와 해결책이 리뷰어에게 높은 점수를 받았다는 증거라고 생각할 수 있겠습니다. 그러면 논문이 말하는 문제와 문제 해결법에 대해 알아보도록 하죠.
Introduction
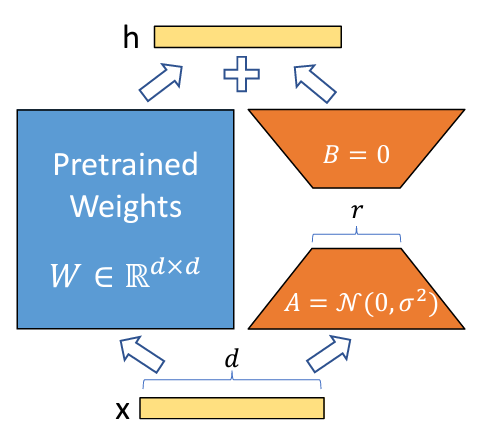
위 그림은 LoRA의 그림입니다. 다들 아시다시피 LoRA의 hidden state $h$는 원본 가중치 행렬 $W_0$와 원본 가중치 행렬을 근사하는 두 작은 행렬의 곱 $BA$에 각각 인풋 $x$를 곱한 결과를 더해 계산됩니다.
이때, 원본 행렬 W_0는 쿼리, 키, 벨류, 임베딩, 피드포워드 같은 일반적으로 Dense 또는 Linear 라고 불리는 신경망 중 하나입니다. 그리고 트랜스포머 모델 내에는 이런 Linear 신경망이 모델크기에 따라 다르지만 보통 몇백개 정도가 있습니다. (싱글 헤드 하나에 쿼리, 키, 벨류, 임베딩, 피드포워드1, 피드포워드2 Linear layer가 있다면 멀티헤드에서 헤드 갯수와 트랜스포머 레이어 수를 곱하면 대략 계산이 됩니다)
LoRA는 이 수많은 Linear layer에 모두 BA행렬을 근사하여 모든 원본 가중치 행렬을 업데이트 합니다. 하지만 논문의 저자들은 초기 실험을 통해 특정한 레이어 또는 특정 가중치만 업데이트 했을때 모든 가중치 행렬을 업데이트 하는 것 보다 더 좋은 성능을 발휘한다는 것을 발견했습니다.
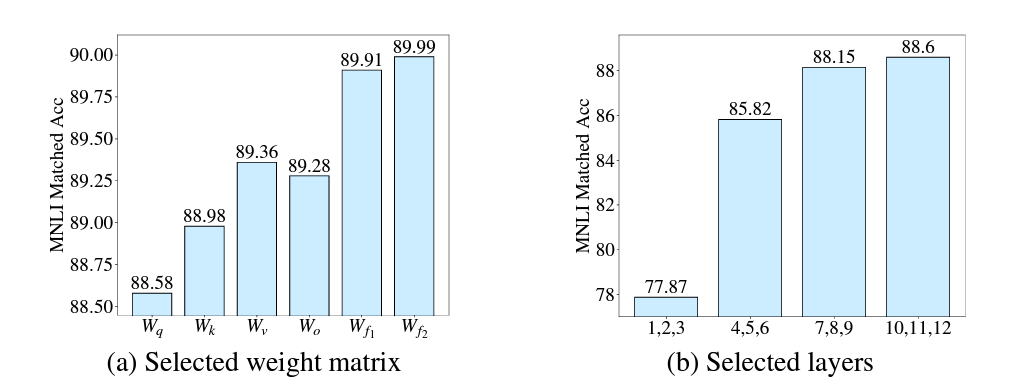
위 그림은 저자들이 특정 가중치 행렬(왼쪽)과 특정 레이어(오른쪽)만 업데이트 한 실험 결과를 나타낸 그림입니다. 보시다시피 피드포워드 가중치 행렬만 업데이트 하거나 상위 레이어만 업데이트할 수록 더 좋은 결과를 보여줍니다. 이에 반해 LoRA는 가중치 간, 레이어 별 중요도를 고려하지 않을 채 모든 컴퓨팅 자원을 동일하게 분배합니다. 이렇게 LoRA 방법으로 fine-tuning을 진행하게 되면 해당 모델은 suboptimal하게 됩니다. 즉, 최적이 아닙니다.
따라서 저자들은 “어떻게 하면 성능에 많은 영향을 주는 가중치 행렬을 선택할 수 있을까?” 하는 의문에 대한 해결책을 제시합니다.
SVD (Singular Value Decomposition)
저자들은 전체 성능에 주요한 영향을 미치는 가중치를 선택하기 위해 SVD 방법에 대해 소개합니다. SVD는 특이값 분해라고도 하는데 어떤 행렬 $A$를 $A=U\Sigma V^T$ 와 같이 분해할 수 있다는 행렬 분해 방법 중 하나입니다. 그리고 이 4가지 행렬은 각각 다음과 같은 크기와 성질을 지닙니다.
$A\in\mathbb{R}^{m\times n}$ : 직사각행렬 (일반적으로 보는 행렬의 모습)
$U\in\mathbb{R}^{m\times m}$ : 직교행렬
$\Sigma\in\mathbb{R}^{m\times n}$ : 대각행렬
$V\in\mathbb{R}^{n\times n}$ : 직교행렬
여기서 직교행렬은 $UU^T = U^TU = I$ 를 만족하는 행렬이고 대각행렬은 대각성분을 제외한 나머지 원소는 0인 행렬을 말합니다.

SVD는 행렬 A를 $A=U\Sigma V^T=\sigma_1\vec{u_1}\vec{v_1}^T+\sigma_2\vec{u_2}\vec{v_2}^T+\cdots+\sigma_n\vec{u_n}\vec{v_n}^T$ 과 같이 행렬 $A$와 크기가 같은 여러개의 행렬로 분해가 가능합니다. 그리고 분해된 각 행렬의 중요도는 $\sigma$에 의해 결정됩니다.
다시말하면 SVD를 통해 임의의 행렬 $A$를 정보량에 따라 여러 행렬로 분해할 수 있습니다!
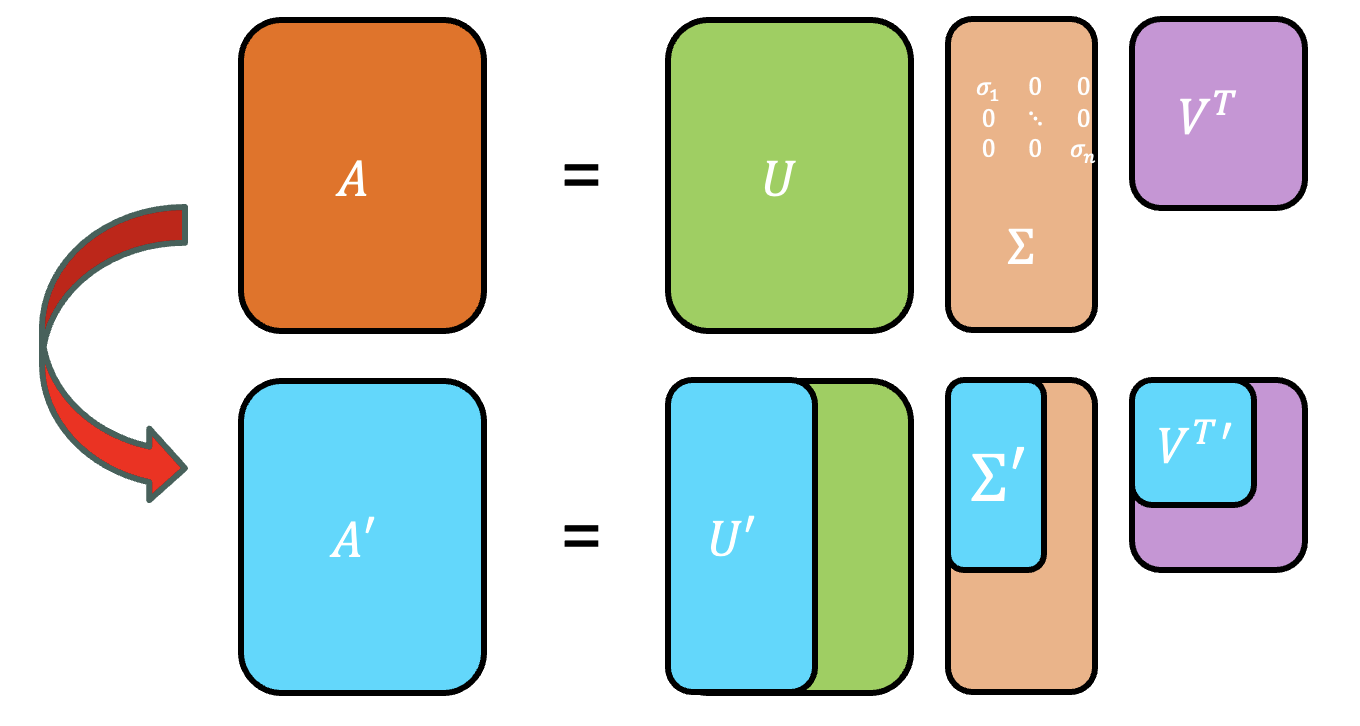
SVD는 SVD로 분해한 행렬을 원본 행렬을 복원하는데 이미 많이 활용되어 왔습니다. 특히 이미지 처리에서 이미지의 용량은 줄이면서 화질의 손상도 줄여주는 압축 복원 방법에 널리 사용되었습니다. 위 그림 처럼 $\Sigma$ 행렬의 대각 원소 크기가 큰 순으로 이미지를 복원하면 더 적은 정보로도 원본 사진을 복원할 수 있습니다.
SVD에 대한 더 자세한 설명은 저보다 똑똑하신 분들께서 이미 많이 해놓았기 때문에 본 논문에서 어떤식으로 접근하는지 정도로만 설명하고 넘어가도록 하겠습니다. 궁금하신 분들은 다음 링크를 참고하여 더 공부해보세요.
- 공돌이의 수학정리노트 (Angelo’s Math Notes) - 특이값 분해(SVD)
- [선형대수학 #4] 특이값 분해(Singular Value Decomposition, SVD)의 활용
하지만 본 논문에서는 SVD를 그대로 활용하지는 않았습니다. 왜냐하면 SVD는 엄청나게 비싼 계산이기 때문이죠. 가중치 행렬 $W\in\mathbb{R}^{d_1\times d_2}$의 SVD 분해를 계산하기 위한 시간복잡도는 $O(min(d_1, d_2)d_1d_2)$ 입니다. 일반적으로 $d_1$과 $d_2$가 같다고 치면 무려 세제곱짜리 시간복잡도를 가지는 셈입니다😱
이런 이유로 논문에서는 SVD 기반의 새로운 가중치 행렬 근사 방법을 제시합니다.
Method
SVD-based adaptation
이전의 LoRA의 개선작들과 마찬가지로 AdaLoRA역시 원본 가중치 행렬을 근사하는 방법 자체는 굉장히 직관적이고 간단합니다. AdaLoRA는 다음 수식을 통해 원본 가중치 행렬을 근사합니다.
\[W=W^{(0)}+\Delta=W^{(0)}+P\Lambda Q\]위 수식에서 $P\in\mathbb{R}^{d_1\times r}$ 과 $Q\in\mathbb{R}^{r\times d_2}$ 는 각각 singular vector를 의미하고 대각행렬 $\Lambda\in\mathbb{R}^{r\times r}$은 singular value를 대각성분으로 가지고 있습니다. 그리고 대각행렬 $\Lambda$는 단일 벡터 ${\lambda_i}_{1\ge i\ge r}$로 줄여서 저장할 수 있고 rank를 의미하는 $r$은 $d_1, d_2$보다 훨씬 작은 값($r\ll min(d_1,d_2)$)을 가집니다.
비교적 간단한 수식입니다. LoRA와 비교하자면 근사행렬 중간에 r차원의 벡터가 하나 더 들어간 셈입니다. 하지만 $P$ 행렬과 $Q$ 행렬이 직교행렬이라는 SVD의 특성을 따라하기 위해 로스식에 다음 규제항을 추가해 줍니다.
\[R(P,Q)=||P^TP-I||_F^2+||QQ^T-I||_F^2\]참고로 위 식의 L2 norm에서 $F$는 프로베니우스(Frobenius)놈으로 벡터가 아닌 행렬에서도 똑같이 L2 norm을 적용하는 방식입니다. 이렇게 AdaLoRA는 SVD를 직접 계산하지 않고 서서히 업데이트 해가는 식으로 SVD와 같은 효과를 볼 수 있게 되었습니다!
그런데 AdaLoRA와 LoRA와의 수식적 차이점은 단지 중간에 r차원의 벡터가 곱해진다는 차이밖에 없기 때문에 LoRA에서 그냥 중간 차원을 없애면 되는것이 아니냐고 물을 수 있습니다. 즉 LoRA의 근사행렬 $BA$에서 rank를 하나 줄이는 것이죠. 이에대해 저자들은 다음과 같은 차이점이 있다고 대답합니다.
1) LoRA의 근사 행렬을 pruning하는 것은 해당 rank를 만드는 행렬$A$와 $B$의 벡터 하나씩을 모두 0으로 만듭니다. 이것은 추후에 이 rank가 더 가치가 있다고 판단되어도 되돌릴 수가 없습니다. 하지만 AdaLoRA는 단지 $\Lambda$ 행렬의 한 성분을 0으로 바꾸는 것이기 때문에 원래 rank값을 언제든지 재활용 할 수 있습니다.
2) LoRA의 근사 행렬 $BA$는 서로 orthogonal(직교)하지 않기 때문에 해당 rank를 pruning하면 다른 rank에도 영향을 미칠 수 있습니다. 하지만 AdaLoRA는 서로 orthogonal하기 때문에 pruning을 해도 다른 rank에 영향을 주지 않습니다.
Importance-aware rank allocation
그렇다면 이제 어떻게 자원을 분배할지, 즉 어떤 가중치 행렬을 더 많이 업데이트 할 지 정하는 알고리즘이 필요합니다. 어떤 행렬이 더 중요한지 나타내는 수치가 바로 $\Lambda$ 행렬에 들어있다고 얘기를 했었는데요. 논문의 저자들은 트랜스포머의 모든 가중치 행렬 $W_q,W_k,W_v,W_{f1},W_{f2}$에 대해, 그리고 모든 헤드와 모든 레이어에 포함된 각각의 가중치 행렬 중 어떤 rank를 살릴 것이고 어떤 rank에 0을 대입해서 사용하지 않을지 정하는 알고리즘을 소개합니다. 요약해서 말씀드리면 이해가 어려우실테니 어서 수식으로 이해해 보도록 하죠!
우선 논문에서 입력으로 들어가는 인풋 데이터 트리플렛 $\mathcal{G}_i=\{P_{\ast i} , \lambda_i , Q_{i\ast}\}_{1\le i\le r}$ 은 하나의 행렬에 랭크의 갯수만큼 분해된 각각의 행렬을 뜻합니다. 여기서 $\ast i$는 $i$번째 열을, $i\ast$는 $i$번째 행을 의미하며 $\lambda_i$는 $\Lambda_{ii}$와 같습니다. 데이터 트리플렛 $\mathcal{G}_i$의 값을 모두 곱하면 해당 행렬의 $i$번째 분해된 행렬을 얻을 수 있습니다.
그런데 위에서 트랜스포머의 모든 가중치 행렬에 대해 모두 실험을 진행한다고 했으므로 이러한 가중치 행렬$\Delta$ 가 $n$개 있다고 가정한다면 $\Delta_k = P_k\Lambda_kQ_k$ ($k=1,…,n$)의 최종 데이터 트리플렛은 다음과 같게 됩니다.
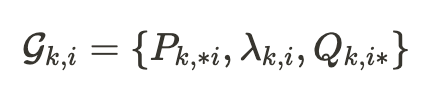
위 데이터 트리플렛을 한번 더 해석해 보자면 $k$번째 가중치 행렬의 $i$번째 rank를 나타내는 행렬을 분해한 left/right singular vector와 singular value 입니다!
그리고 논문에서 그레디언트를 표현하기 위해 로스식을 다음과 같이 정의합니다.
\[\mathcal{L(P,E,Q)=C(P,E,Q)}+\gamma\sum_{k=1}^n R(P_k,Q_k)\]여기서 $\mathcal{P}=\{P_k\}_{k=1}^n, \mathcal{E}=\{\Lambda_k\}_{k=1}^n, \mathcal{Q}=\{Q_k\}_{k=1}^n$ 이고 $\mathcal{C(P,E,Q)}$는 학습 비용을 나타냅니다. 그리고 $\gamma$는 정규화계수로 0보다 큰 값을 가지게 됩니다.
그렇다면 우리는 $t$번째 스텝에서 $\Lambda_k$에 대해 다음과 같이 확률적 그레디언트(stochastic gradient)를 구할수 있게 됩니다.
\[\tilde\Lambda_k^{(t)}=\Lambda_k^{(t)}-\eta\nabla_{\Lambda_k}\mathcal{L(P,E,Q)}\]여기서 $\eta$는 0보다큰 학습률(learning rate)를 의미합니다. 마찬가지로 $P, Q$도 똑같이 업데이트 합니다만 특별히 $\Lambda$는 총 파라미터 자원인 budget을 관리하기 위한 알고리즘을 추가하기 위해 $\tilde\Lambda_k^{(t)}$를 활용합니다.
$\tilde\Lambda_k^{(t)}$를 구하고난 후 중요도 점수(Importance score)인 $S_k^{(t)}$가 주어지면 singular value는 다음과 같이 pruning됩니다.
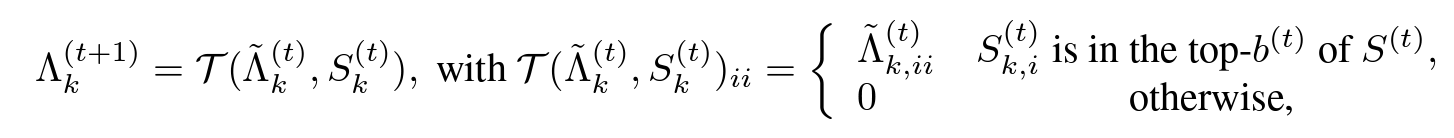
여기서 $S^{(t)}={S_{k,i}^{(t)}}_{1\le k\le n,1\le i\le r}$ 이고 모든 트리플렛의 importance score을 포함합니다. 그리고 $b^{(t)}$는 $t$번째 스텝에서 남아있는 singular value의 budget입니다. 다시한번 위 식을 해석해 보자면, 다음 스텝의 singular value는 $\mathcal{T}(\cdot)$에 의해 결정됩니다. $\mathcal{T}(\cdot)$은 importance score를 보고 해당 rank가 남아있는 순위안에 들면 그대로 singular value를 남기고, 아니면 0을 주는 간단한 함수입니다.
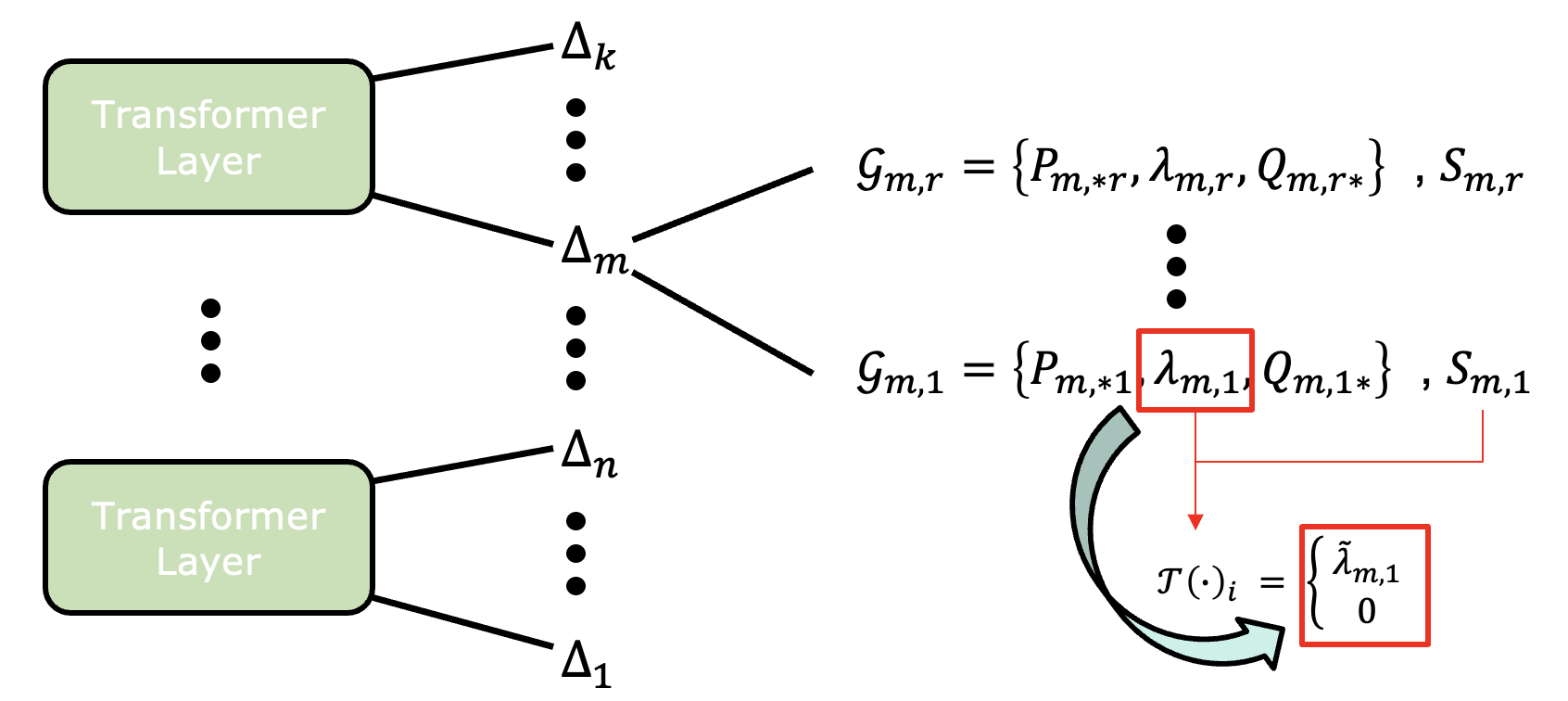
위 그림처럼 트랜스포머 구조와 본 논문에서 다루는 데이터의 한 단위인 트리플렛에 대한 그림이 머릿속에서 그려지시나요? 수많은 트랜스포머 내의 가중치 행렬 하나하나를 또다시 rank의 갯수만큼 행렬을 분해하는 과정만 이해하시면 논문 이해가 쉬워질 것입니다.
그렇다면 마지막으로 스코어를 구하는 방법만 알면 어떻게 $\Lambda$행렬을 통해 budget을 관리하는지 파악할 수 있게 됩니다!
How to calculate importace score
Importance socre를 구하는 방법에는 크게 두 가지가 있습니다.
Magnitude of singular values
이 방법은 가장 직관적인 방법으로써 그냥 singular value의 절대값 크기 자체가 스코어가 되는 경우입니다. SVD를 활용해서 matrix의 rank를 조절하는 이전 연구들에서 이 방법을 사용하고 있습니다. 하지만 이 방법은 해당 singular value가 모델의 성능에 얼마나 영향을 끼치는지는 잘 나타내지 못합니다.
Sentitivity-based importance
이 방법은 어떤 파라미터가 training loss에 많은 영향을 끼치는지 분석한 이전 논문들의 방법론을 AdaLoRA에 맞게 변형한 방법입니다. 이전의 연구들은 파라미터 하나하나가 얼마나 영향을 끼치는지 확인하는 방법이었는데, AdaLoRA는 트리플렛 자체가 얼마나 영향을 미치는지 알면 됩니다. 따라서 임의의 트리플렛 $\mathcal{G}_{k,i}$에 대한 스코어 $S_{k,i}$는 다음과 같습니다.
\[S_{k,i}=s(\lambda_{k,i})+\frac{1}{d_1}\sum_{j=1}^{d_1}s(P_{k,ji})+\frac{1}{d_2}\sum_{j=1}^{d_2}s(Q_{k,ij})\]위 수식을 해석하자면, 스코어는 어떤 스코어 계산 함수 $s(\cdot)$을 통해 계산합니다. 그런데 트리플렛의 총합만 계산하면 되므로 트리플렛 각각에 스코어 계산 함수 $s(\cdot)$를 각각 적용해 줍니다. 그리고 $P_{k,\ast i}, Q_{k,i\ast }$는 벡터이기 때문에 벡터의 크기에 따라 스코어가 변하는 것을 방지하기 위해 평균값을 사용합니다. (벡터 길이가 길다고 스코어가 높거나 낮으면 안되겠죠?)
그렇다면 마지막으로 $s(\cdot)$을 구하는 함수에 대해 알아보면 끝입니다! 본 논문에서는 $s(\cdot)$를 계산하기 위해 다음과 같은 gradient-weight 곱의 절대값을 사용합니다.
\[I(w_{ij})=|w_{ij}\nabla_{w_{ij}}\mathcal{L}|\]여기서 $w_{ij}$는 어떤 파라미터 하나를 의미하고 이 수식은 말그대로 파라미터값 하나와 그 파라미터의 그레디언트를 곱한 값의 절대값 입니다. 이것이 의미하는 바는 현재 변화율(미분값)을 통해 0부터 해당 파라미터까지 움직인 값을 근사하겠다는 것입니다. (함수가 선형적이라면 완벽하게 똑같을 것입니다.) 그래서 이 값은 로스에 대한 변화율이 클 수록, 원래 파라미터가 가지고 있는 값이 클 수록 더 높은 값을 가지게 됩니다.
하지만 Platon: Pruning large transformer models with upper confidence bound of weight importance (ICML, 2022) 논문에서 위 식은 mini-batch로 학습하는 모델에서는 너무 큰 변동성과 불확실성을 가지고 있어서 위 식을 sensitivity smoothing과 uncertainty quantification을 통해 추정합니다. 따라서 참조한 논문의 방법을 따라 본 논문에서도 다음과 같이 sensitivity smoothing과 uncertainty quantification을 적용합니다.
\[\overline{I}^{(t)}(w_{ij})=\beta_1\overline{I}^{(t-1)}(w_{ij})+(1-\beta_1)\overline{I}^{(t)}(w_{ij})\] \[\overline{U}^{(t)}(w_{ij})=\beta_2\overline{I}^{(t-1)}(w_{ij})+(1-\beta_2)|I^{(t)}(w_{ij})-\overline{I}^{(t)}(w_{ij})|\]여기서 $\beta_1$, $\beta_2$는 0과 1사이의 값입니다. 위 수식을 다시 살펴보자면 $\overline{I}^{(t)}$는 지수 이동 평균을 통해 smoothing 한 값이고 $\overline{U}^{(t)}$는 $\overline{I}^{(t)}$과 ${I}^{(t)}$의 불확실성을 측정한 값입니다. 마지막으로 $s(\cdot)$을 구하기 위해서는 다음과 같이 $\overline{I}^{(t)}$과 $\overline{U}^{(t)}$를 곱해주면 됩니다.
\[s^{(t)}(w_{ij})=\overline{I}^{(t)}\cdot\overline{U}^{(t)}\]이렇게 AdaLoRA가 어떻게 SVD기반의 행렬 근사를 수행하며 어떻게 총 파라미터 budget을 관리하는지 알게되었습니다! 한번에 알아보기 쉽게 저자들이 알고리즘도 제시해 줬습니다.
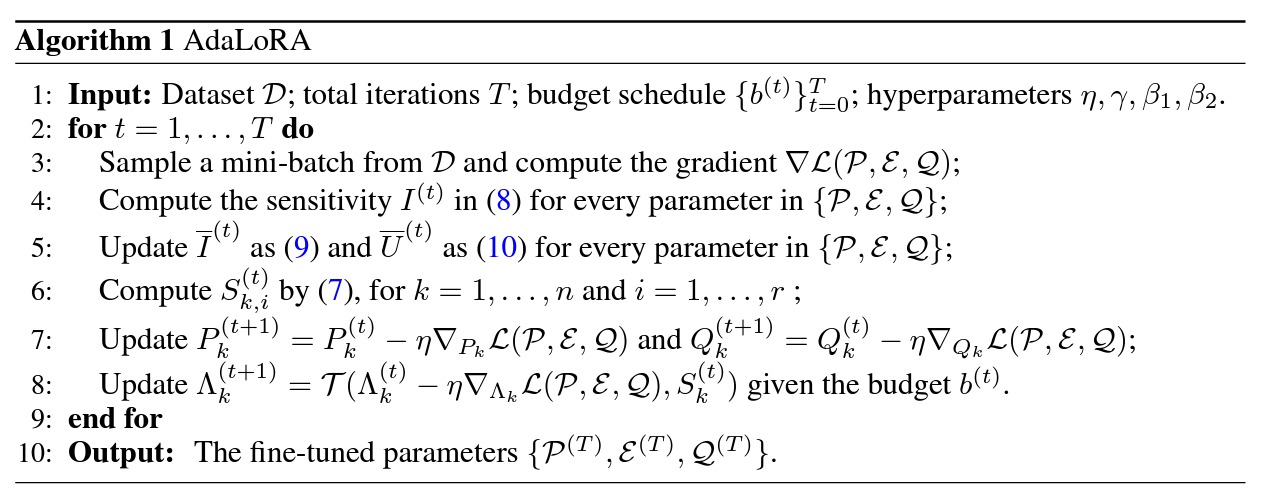
위 알고리즘에서 4~6번 라인이 triplet별 score를 계산하는 부분이고 8번 라인이 singular value를 pruning하는 과정 입니다. 마지막으로 파인튜닝이 완료된 프리플렛 셋을 리턴합니다.
Global budget scheduler
AdaLoRA의 budget $b^{(T)}$은 가중치 행렬의 총 rank 수, 즉 총 singular vlaue의 개수입니다. budget 할당은 파인 튜닝 과정에서 반복적으로 수행하는데, 훈련을 좀 더 용이하게하기 위해 새롭게 제안하는 학습 방법이 global budget scheduler 입니다.
global budget scheduler은 초기 budget $b^{(0)}$을 목표 budget $b^{(T)}$보다 약 1.5배 높게 설정합니다. 각 가중치 행렬의 초기 rank수를 $r = b^{(0)}/n$으로 설정합니다. 훈련을 $t$단계 동안 워밍업하고, 그런 다음 예산 $b^{(t)}$가 $b^{(T)}$에 도달할 때까지 예산을 감소시키는 cubic 스케줄( $value(t)=initial\_value\times(1−\frac{t}{total\_steps})^3$ )을 따릅니다.
이를 통해 AdaLoRA는 학습할때 먼저 파라미터 공간을 탐색한 다음 가중치 변화에 집중할 수 있게됩니다.
Experiments
실험부분에는 많은 실험이 있지만 주요한 실험만 몇개 보고 넘어가겠습니다. 실험 방법과 설정에도 중요한 정보가 많으니 실제로 한번 꼭 읽어보시기 바랍니다.
GLUE benchmark
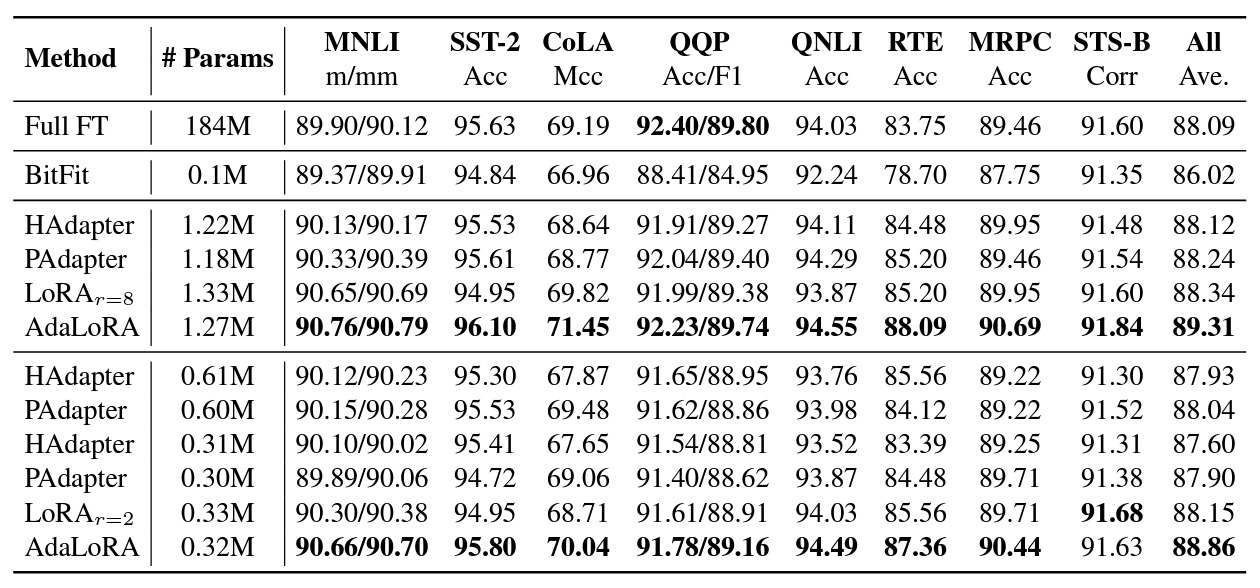
DeBERTa V3-base 모델로 GLUE 벤치마크를 돌린 결과입니다. 대부분의 경우에 baseline 모델들 보다 더 좋은 성능을 보입니다.
Question answering
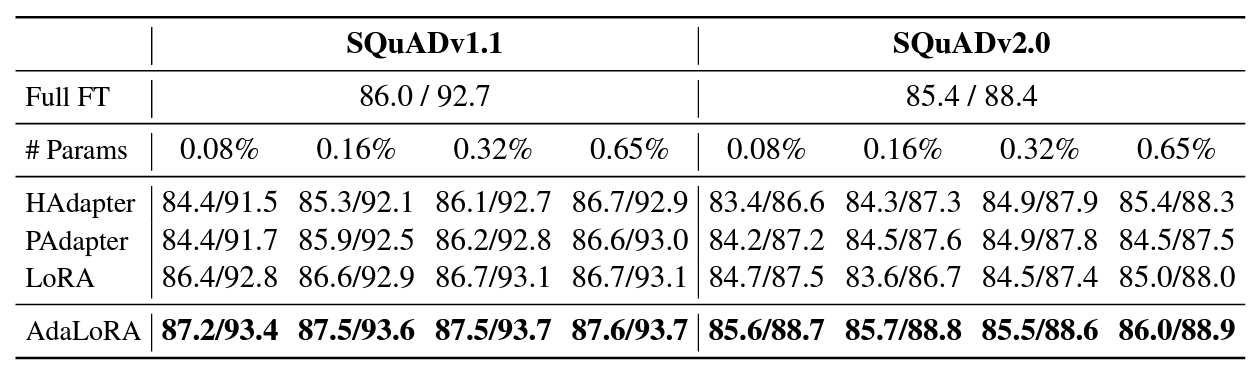
QA의 대표 데이터셋인 SQuAD 데이터셋에서도 가장 좋은 성능을 보여주고 있습니다.
Variants of the importance score
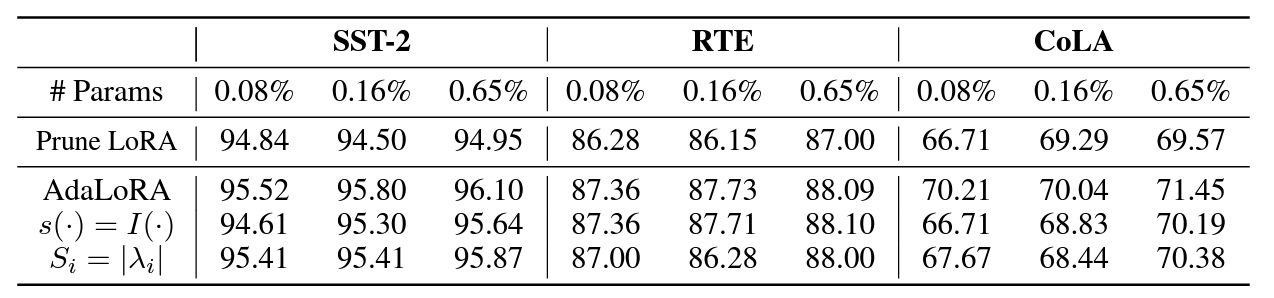
Importance socre 방법에 따른 ablation study입니다. 본 논문에서 제시한 방법을 썼을때가 가장 좋은 성능을 발휘합니다.
Ablation studies about SVD-based adaptation and budget allocation
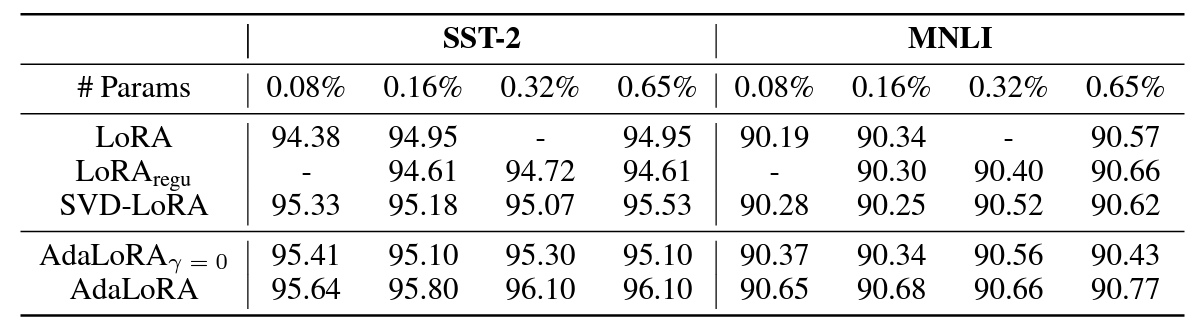
SVD-based adaptation을 사용하는 것과 안하는것, budget allocation을 사용하는 것과 안하는것, 그리고 orthogonal regularization을 사용하는 것과 안하는것의 차이로 볼 때 전부 적용한 AdaLoRA가 가장 성능이 좋음을 알 수 있습니다.
The resulting budget distribution
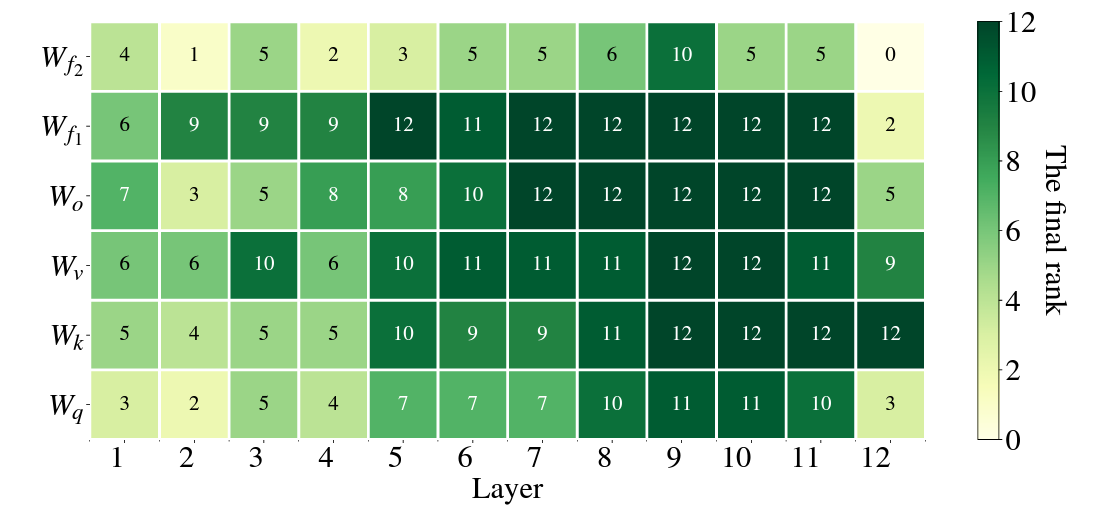
마지막으로 어떤 레이어에 어떤 가중치 행렬에 더 많은 rank가 할당되었는지 보여주는 맵입니다. 상술했듯이 feedforward 혹은 임베딩 행렬 쪽으로 갈수록 중요도가 높으며, 상위 레이어로 갈 수록 중요도가 더 높음을 알 수 있습니다.
Conclusion
AdaLoRA는 효율적인 파라미터 할당을 위한 새로운 방법을 제시하였습니다. AdaLoRA는 SVD 기반의 행렬 근사를 통해 가중치 행렬을 각각 랭크 행렬 분해하고, 각 랭크의 중요도에 따라 파라미터를 할당합니다. 이를 통해 모델의 파인튜닝 성능을 최적으로 높이면서 메모리 사용량을 줄일 수 있었습니다.
이상으로 AdaLoRA에 대한 소개를 마치겠습니다. AdaLoRA를 활용하면 기존의 방법보다 효율적으로 트랜스포머 모델을 파인튜닝하면서 메모리 사용량을 줄일 수 있습니다. 이로써 더 많은 연구자들이 대규모 트랜스포머 모델을 활용하여 다양한 연구를 수행할 수 있는 새로운 가능성이 열렸습니다. 다음에도 새로운 연구와 기술에 대한 소개를 계속해 나가겠습니다. 봐주셔서 감사합니다🤗
잘못된 점에 대한 피드백은 언제나 환영입니다.