LLM의 input및 output 토큰별 FLOPS와 전력 소모량 계산

안녕하세요 jiogenes 입니다.

오늘은 LLM의 토큰별 연산량과 그에따른 전력소모량을 추정할 수 있는 방법에 대해 알아보겠습니다.

Introduction

바야흐로 비싼 GPU만 있으면(혹은 클라우드를 돌릴 돈이 충분하다면) 여러종류의 오픈소스 대규모 LLM을 로컬로 편하게 돌려볼 수 있는 시대가 되었습니다. 하지만 LLM은 절대 공짜로 돌아가는게 아닙니다! GPU를 살때도 비싸지만 바로 전기를 어마어마하게 먹기 때문입니다. OpenAI가 구독료를 많이 받음에도 불구하고 계속해서 적자를 보는것도 GPU 구매 비용 뿐만 아니라 유지비용이 상당히 많이 들기 때문입니다.

그렇다면 도대체 얼마나 전기를 먹길래 이렇게 호들갑일까 궁금합니다. 따라서 GPU 메모리를 충분히 확보했다고 쳤을 때, 얼마나 전력을 소모하는지에 대해 알아보는 시간을 가져보도록 하겠습니다.

FLOP 및 FLOPS 개념

FLOPS를 이해하기 위해 먼저 FLOP에 대해 간단히 알아보겠습니다. [1]

FLOP(Floating Point Operation)이란 부동 소수점 연산 횟수를 의미합니다. 예를 들어, 0.3 + 0.7 이라는 연산이 실행되면 FLOP은 1이됩니다. 즉, 한 번의 부동 소수점 연산이 발생한 것입니다.

반면, FLOPS(Floating Point Operations per Second; FLOPs, FLOP/s)는 초당 수행되는 부동 소수점 연산의 횟수를 나타냅니다. 이는 컴퓨터 성능을 측정하는 중요한 지표로, 특히 대형 언어 모델(LLM)과 같은 복잡한 계산에서 많이 사용됩니다.

이번 포스팅에서 핵심적으로 다룰 개념은 FLOPS/token입니다. 이는 토큰 하나당 얼마나 많은 FLOPS가 필요한지를 계산하는 것으로, LLM이 각 토큰을 처리할 때 요구되는 연산량을 평가하는 중요한 기준이 됩니다. 연산량을 파악한 후 최대 연산량 대비 최대 전력소모량을 곱해주면 토큰별 최대 전력소모량을 알 수 있습니다.

LLM의 FLOPS 계산 추정

LLM은 transformer를 사용하므로 transformer의 FLOPS를 계산해보도록 하겠습니다.

먼저, 아주 naive하게 근사하자면 모델의 총 파라미터를 $N$, 모델에 입력되는 token 길이를 $D$ 라고 할 때, 총연산량 $C$는 다음과 같습니다. [2]

$C \approx 6ND$

위 근사값은 다음과 같은 이유로 계산됩니다.

파라미터 $i$에서 파라미터 $j$로 forward할 때, 가중치 $w$를 곱하는 부동소수점 연산 1회
파라미터 $j$에 연결된 다른 파라미터로부터 forward된 값을 모두 더할 때, 부동소수점 연산 1회
파라미터 $j$에서 파라미터 $i$로 backward할 때, 활성화 함수의 미분을 계산하는 부동소수점 연산 1회
파라미터 $i$에 연결된 다른 파라미터로부터 backward된 모든 활성화 손실 값을 더할 때, 부동소수점 연산 1회
파라미터 $j$에 연결된 가중치의 미분을 계산하기 위해 부동소수점 연산 1회
파라미터 $i$에 연결된 가중치들에서 들어온 모든 미분 값을 더할 때, 부동소수점 연산 1회

그러나 이 근사값에는 몇 가지 문제점이 있습니다.

첫째, 우리는 학습을 하지 않습니다! Bigtech 기업에서 모델 학습에 관련된 부서에 속하지 않는 한, 대형 모델을 학습하기에는 하드웨어와 비용이 절대적으로 부족합니다. 또한, SLM을 학습하는 것보다 LLM이 대부분 그 역할을 대체할 수 있기 때문에 점점 의미가 줄어들고 있습니다. 우리가 집중해야 할 것은 LLM 추론으로 어떤 응용을 할 수 있는가 입니다. 따라서, 추론 시의 연산량만을 고려하는 것이 적절합니다. 추론에는 backward에 대한 연산이 없으므로 최종 근사값은 $2ND$가 될 것입니다.

둘째, Transformer 내부의 self-attention 계산에 필요한 연산은 고려되지 않았습니다. 이는 파라미터(가중치)를 가지지 않고, 계산된 QKV를 사용해 별도로 연산하기 때문입니다. 따라서 self-attention 내부의 연산량을 고려하면 좀 더 정확히 transformer의 연산량을 추정할 수 있습니다.

셋째, prompt를 입력할 때와 token을 생성할 때의 연산량이 서로 다릅니다. LLM은 대부분 decoder-only 모델이기 때문에 토큰 생성시의 self-attention 연산은 절반을 없앨 수 있습니다. token generation을 위해 decode를 할 때 대부분의 LLM이 one-by-one step으로 다음 토큰을 계산하기 때문에 self-attention연산이 모든 토큰이 한번에 들어온 것 처럼 계산될 수 없습니다. 반대로, 프롬프트를 입력할 때는 사용자가 입력하는 프롬프트를 한번에 넣어주기 때문에 self-attention을 한번에 계산할 수 있습니다.

Transformer 한 layer의 FLOPS 계산

Notation 및 Transformer 내부 계산시 사용되는 행렬의 shape

FLOPS 계산에 있어 Notation을 정리하겠습니다.

$d_{model}$: model size, hidden state의 차원

$d_{head}, d_{q}, d_{k}, d_{v}$: head 하나 당 출력 차원($d_{head} \times n_{head} = d_{model}$)

$n_{head}$: multi head attention의 head 갯수

$n_{layer}$: transformer layer 갯수

$n_{seq}$: sequence 길이

$X^n \in \mathbb{R}^{n_{seq} \times d_{model}}$: n번째 layer의 hidden state 벡터

$W_q^n \in \mathbb{R}^{d_{model} \times d_{model}}$: n번째 layer의 query 가중치 행렬

$W_k^n \in \mathbb{R}^{d_{model} \times d_{model}}$: n번째 layer의 key 가중치 행렬

$W_v^n \in \mathbb{R}^{d_{model} \times d_{model}}$: n번째 layer의 value 가중치 행렬

$W_o^n \in \mathbb{R}^{d_{model} \times d_{model}}$: n번째 layer의 output 가중치 행렬

$W_{ff1}^n \in \mathbb{R}^{d_{model} \times 4d_{model}}$: n번째 layer의 첫번째 피드포워드 가중치 행렬

$W_{ff2}^n \in \mathbb{R}^{4d_{model} \times d_{model}}$: n번째 layer의 두번째 피드포워드 가중치 행렬

원래는 batch size도 함께 고려해야 하지만, inference시에는 batch size가 보통 1이므로 생략합니다.

밑의 pseudo code를 통해 FLOPS를 계산해 봅시다.

def transformer_layer(X): # [n_seq, d_model]
  X = X + multi_head_attention(X) # [n_seq, d_model]
  X = X + feed_forward_network(X) # [n_seq, d_model]
  X = layer_norm(X) # [n_seq, d_model]
  return X # [n_seq, d_model]

def multi_head_attention(X): # [n_seq, d_model]
  Q = X.matmul(W_q) # [n_seq, d_model] * [d_model, d_model]
  K = X.matmul(W_k) # [n_seq, d_model] * [d_model, d_model]
  V = X.matmul(W_v) # [n_seq, d_model] * [d_model, d_model]
  O = [self_attention(
        Q[..., (i-1)*d_head:i*d_head], # [n_seq, d_q]
        K[..., (i-1)*d_head:i*d_head], # [n_seq, d_k]
        V[..., (i-1)*d_head:i*d_head]) # [n_seq, d_v]
      for i in n_head]
  O = concat(O, dim=-1).matmul(W_o) # [n_seq, d_model]
  return X # [n_seq, d_model]

def self_attention(Q, K, V): # [n_seq, d_head] respectively
  score = Q.matmul(K.T) / sqrt(d_head) # [n_seq, d_q] * [d_k, n_seq]
  output = softmax(score, dim=-1).matmul(V) # [n_seq, n_seq] * [n_seq, d_v]
  return output # [n_seq, d_head]

def feed_forward_network(X): # [n_seq, d_model]
  X = X.matmul(W_ff1) # [n_seq, d_model] * [d_model, 4*d_model]
  X = relu(X) # [n_seq, 4*d_model]
  X = X.matmul(W_ff2) # [n_seq, 4*d_model] * [4*d_model, d_model]
  return X # [n_seq, d_model]

행렬 곱셈의 FLOPS 계산

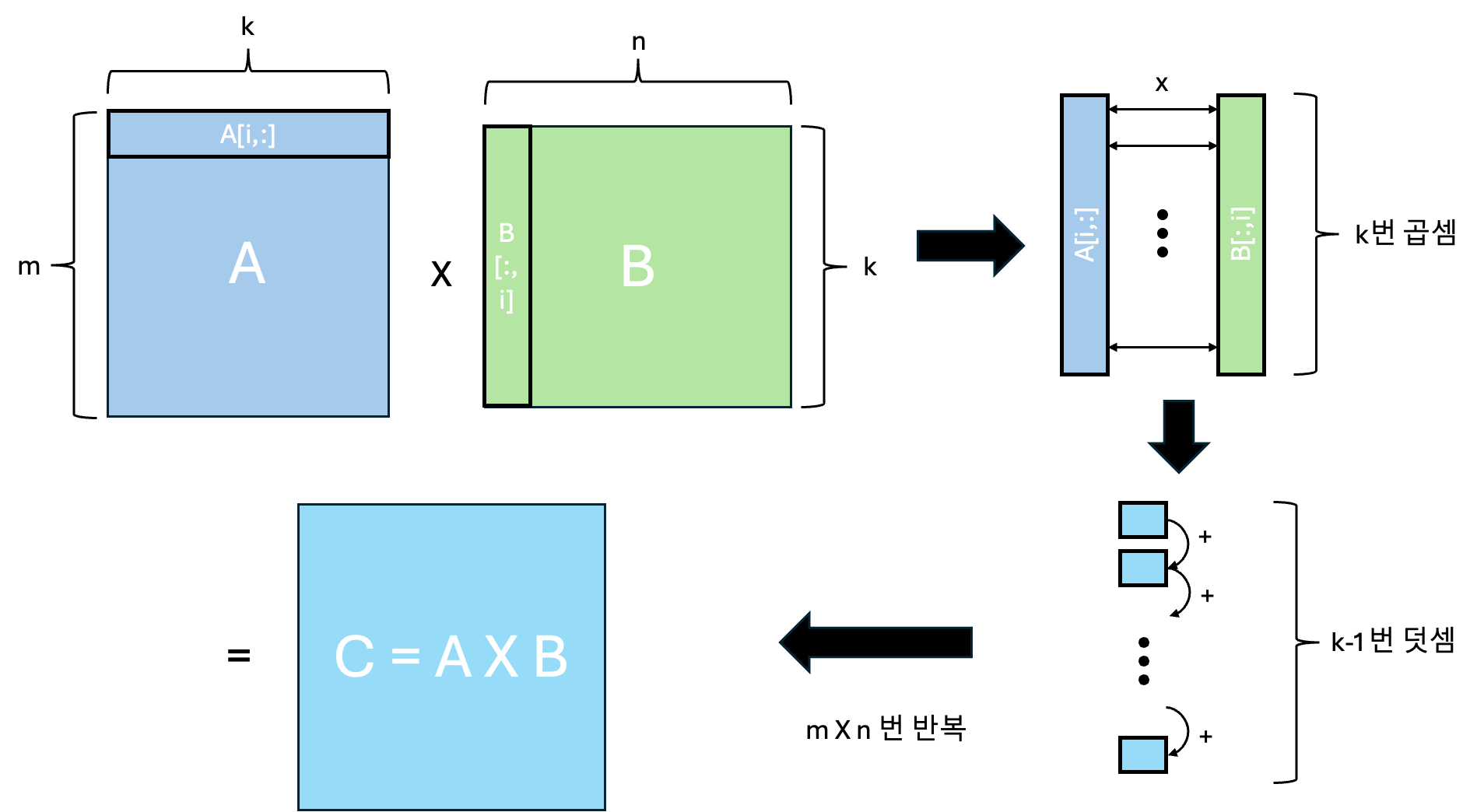
행렬 곱셈(matrix multiplication) 연산에서는 직관적으로 $m×k$ 행렬과 $k×n$ 행렬을 곱할 때, $m \times k \times n$번의 연산이 발생합니다. 그러나 NVIDIA CUDA에서는 이 행렬 연산을 곱셈과 덧셈 연산으로 나누어 실행하기 때문에, 총 $2 \times k \times m \times n$ 번의 연산이 이루어집니다 [5]. 예를들어, $C\in \mathbb{R}^{m \times n}=A\in \mathbb{R}^{m \times k} \times B\in \mathbb{R}^{k \times n}$ 라는 연산을 한다면,

dot-product 연산을 위해, A 행렬의 한 row와 B 행렬의 한 column의 곱셈 연산이 element-wise로 $k$번 일어납니다.
곱해진 각각의 k개의 element들이 k번 더해집니다. (정확히는 k-1번 더해집니다!)
위 연산이 총 $m \times n$ 번 일어납니다.

그렇다면 우리가 궁금해하는 transformer의 한 레이어에 대한 FLOPS를 계산해봅시다.

Transformer의 FLOPS

MHA FLOPS

multi*head_attention 함수에서는 QKVO를 만들기 위한 행렬 곱셈 연산이 수행됩니다. (matmul 메소드가 실행되는 부분을 보시면 됩니다!) 위 행렬 곱셈의 FLOPS 계산을 참고하면 각각의 QKVO의 FLOPS는 $2 \times n_{seq} \times d_{model} \times d_{model}$ 입니다. QKVO는 각각 같은 같은 크기의 행렬 곱셈이 이뤄지므로 최종적으로 $8 \times n_{seq} \times d_{model}^2$가 되겠네요.

Self attention FLOPS

마찬가지로 self*attention 함수 내부의 matmul 연산을 살펴보면, $2 \times n_{seq} \times n_{seq} \times d_{head}$ 연산이 총 2번 일어나므로 $4 \times n_{seq}^2 \times d_{head}$가 될것입니다.

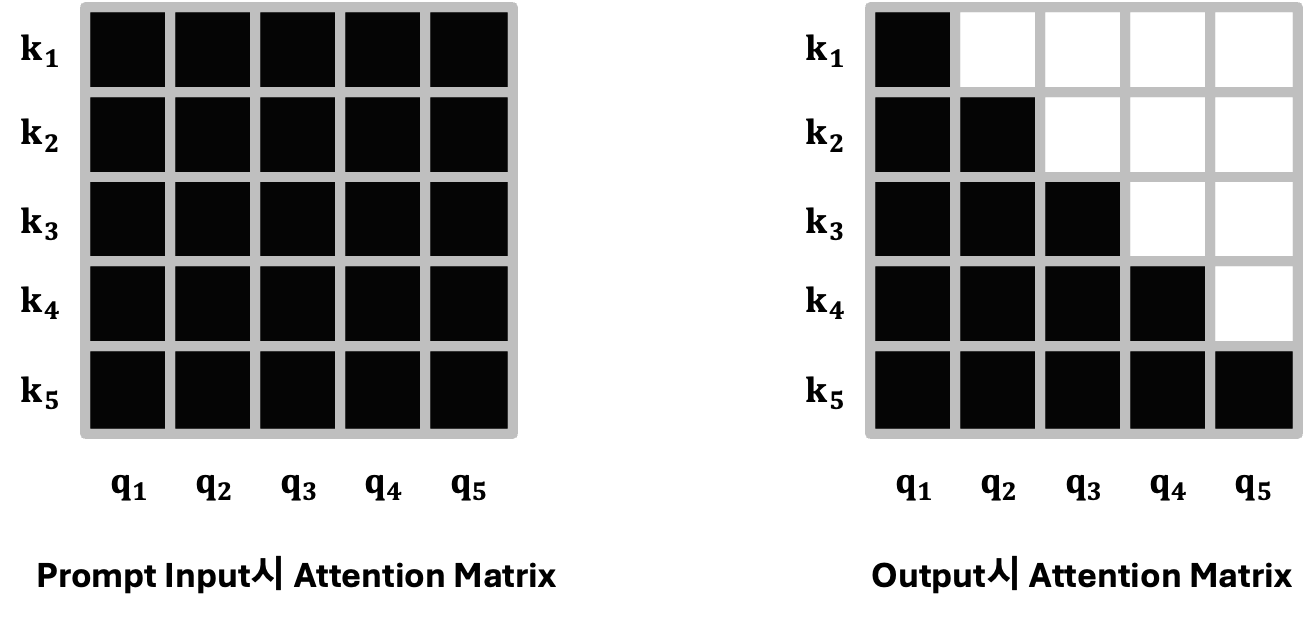
하지만 위에서 FLOPS 근사값 추정에서 말씀드렸듯이 prompt 입력을 처리할 때와 token을 생성하는 과정에서 self-attention 연산량에 차이가 있습니다. 바로 위에서 계산한 연산량은 입력된 prompt의 모든 토큰이 한번에 계산될 때의 연산량이며, 다음 token을 예측하는 decoding 시에는 이전에 생성된 토큰들의 self-attention만 차례대로 계산하면 되므로 연산량이 절반으로 줄어듭니다. 따라서 decoding 시 FLOPS는 $2 \times n_{seq}^2 \times d_{head}$이 됩니다. (생성된 token을 합한 시퀀스의 길이가 이전에 생성된 토큰들의 시퀀스 길이보다 1개 더 많으므로 $2 \times (n_{seq} + 1) \times n_{seq} \times d_{head}$로 표현할 수도 있습니다.)

Feed forward network FLOPS

마지막으로 feed_forward_network 함수 내부의 matmul 연산은 $2 \times n_{seq} \times d_{model} \times 4 \times d_{model}$ 이며 이것이 총 2번 이뤄지므로 $16 \times n_{seq} \times d_{model}^2$가 됩니다.

Layer norm, softmax, RELU 그 외

layer norm과 softmax, relu도 각각 연산이 필요합니다. 각각의 연산을 뜯어보면 layer norm은 $n_{seq} \times d_{model}$, softmax는 $2 \times n_{seq} \times d_{head}$, RELU는 $4 \times n_{seq} \times d_{model}$입니다. 다른 matmul FLOPS와 비교해 제곱 항이 없으므로 크기가 커지면 커질수록 그 영향이 적기 때문에 무시할 수 있습니다.

또한, dropout, token embedding, positional embedding도 모두 연산량을 요구하지만 제곱항에 비해 무시할 수 있는 수준이기 때문에 생략합니다.

Transformer의 토큰별 FLOPS 계산

단일 layer 상에서 FLOPS를 계산했으니 이제 해당 모델의 layer 수인 $n_{layer}$를 곱해주면 모델의 최종 FLOPS를 계산할 수 있습니다. 그리고 토큰별 FLOPS를 계산하기 위해 총 FLOPS 에서 $n_{seq}$ 을 나눠주면 토큰별 FLOPS를 계산할 수 있습니다!

$\begin{align} \text{FLOPS}\_{MHA}&=n\_{layer} \times 8 \times d\_{model}^2 \\ \text{FLOPS}_{ATTN_{input}}&=n\_{layer} \times 4 \times n\_{seq} \times d\_{model} \\ \text{FLOPS}\_{ATTN\_{output}}&=n\_{layer} \times 2 \times n\_{seq} \times d\_{model} \\ \text{FLOPS}\_{FFN}&=n\_{layer} \times 16 \times d\_{model}^2 \\ \end{align}$

그리고 최종적으로 Transformer의 FLOPS는 다음과 같습니다.

$FLOPS = \begin{cases} n_{layer} \times (24 \times d_{model}^2 + 4 \times n_{seq} \times d_{model}), & \text{ for input tokens}\\ n_{layer} \times (24 \times d_{model}^2 + 2 \times (n_{seq}+1) \times d_{model}), & \text{for output tokens}\\ \end{cases}$

위에서 봤던 $2ND$ 의 근사값과 비교해보자면, $N$은 총 파라미터 수 이므로 모든 가중치 행렬의 크기를 더한 $n_{layer} \times 12 \times d_{model}^2$이 될 것입니다.

\[\|W_q\| + \|W_k\| + \|W_v\| + \|W_o\| + \|W_{ffn1}\| + \|W_{ffn2}\| = 12 \times d_{model}^2\]

따라서 $2ND=n_{layer} \times 24 \times d_{model}^2$는 총 연산량에서 self-attention 연산을 제외한 근사값임을 알 수 있습니다.

Transformer의 토큰별 전력 소비량 계산

대규모 LLM을 예시로 들었기 때문에 최근에 나온 LLAMA3.1 70B 모델과 NVIDIA A100 1장을 기준으로 전력 요구량을 계산해보겠습니다. (사실 70B 모델을 양자화 하지 않으면 A100 1장으로는 돌리기는 어렵습니다….)

하드웨어 성능 및 모델 사이즈 계산

LLM을 inference할 때 일반적으로 half-precision(FP16)을 사용하며, A100의 최대 FP16 FLOPS는 312 TFLOPS입니다 [8]. 그리고, LLAMA 3.1 70B 모델의 layer 수는 32, hidden dimension 크기는 4096이므로 [9] 계산해보면 입력과 출력 토큰별 FLOPS는 대략 13e9 정도 됩니다. (학습이 아니고 배치, 레이어놈과 같은 계산도 전부 빠져있기 때문에 조금 작을 수 있습니다. 원래는 이것보다 더 크다고 가정해야 합니다.)

초당 처리 가능 토큰 수 계산

초당 처리 가능한 토큰 수는 GPU성능을 토큰당 FLOPS로 나누면 계산가능합니다.

\[초당 토큰 수=\frac{GPU 성능}{토큰당 FLOPS}\approx\frac{312 \times 10^{12} FLOPS/s}{13 \times 10^9 FLOPS/\text{token}}\approx 24,000 \text{token}/s\]

전력 및 전력 소비량과 전기 요금 계산

NVIDIA의 최대 전력 소비량은 약 300W이며, 토큰당 전력 소비량은 GPU 전력소비량을 초당 토큰 수로 나눠주면 됩니다. 마지막으로, 전기요금은 토큰당 에너지 소비값과 전기 요금 값을 곱하면 계산할 수 있습니다.

전기요금은 한전의 20203년 전력 판매가격 평균가를 기준으로 150원으로 측정하였습니다. [10]

$\begin{align} 토큰당 전력 소비(W)&=\frac{GPU 전력 소비(W)}{초당토큰수} \\ \\ &=\frac{300W}{24,000 \text{token}/s} \\ \\ &\approx 0.0125 W /\text{token} \\ \end{align}$

$\begin{align} 토큰당 전력 소비량(Wh)&=토큰당전력소비(W)\times\frac{1h}{3,600s} \\ \\ &=0.0125 \times \frac{1h}{3,600s} \\ \\ &\approx 0.00000347 Wh/\text{token} \\ \end{align}$

$\begin{align} 토큰당 요금(원)&=토큰당전력소비량(Wh)\times 전기요금{원/kWh}\\ \\ &\approx 0.00000347 Wh/\text{token} \times 150원/kWh\\ \\ &= 0.0005205원/\text{token} \\ \end{align}$

Finally

최대한 간단하게 계산해본 토큰당 LLM 추론 전기 요금은 NVIDA A100 1장, LLAMA 3.1 70B 모델 기준 1000토큰당 약 0.5원 정도라는 결론이 났습니다!

이 계산 결과를 보면 LLM을 사용할 때 전기 요금이 생각보다는 크지 않다는 것을 알 수 있습니다. 하지만 대규모로 LLM을 운영하는 기업의 경우 이 비용이 상당히 클 수 있겠다고 생각이 들었습니다.

왜냐하면 위 계산들은 아주 단순화한 모델 기반이며 배치사이즈나 layer norm과 같은 중요한 계산도 빠져 있습니다. 그리고 실제 서비스시에는 서버 운영 비용, 네트워크 비용, 인건비 등 추가적인 비용이 뒤따릅니다. 특히, openAI에서 쏟아져 들어오는 트레픽을 감당하기 위한 분산처리를 어떻게 하는지 궁금하군요.

이제, 위 수식에 대입해서 여러분이 가진 GPU와 LLM 모델을 가지고 토큰당 전기비용이 얼마나 나올지 계산해 보시기 바랍니다.

읽어주셔서 감사합니다!