안녕하세요 jiogenes입니다.

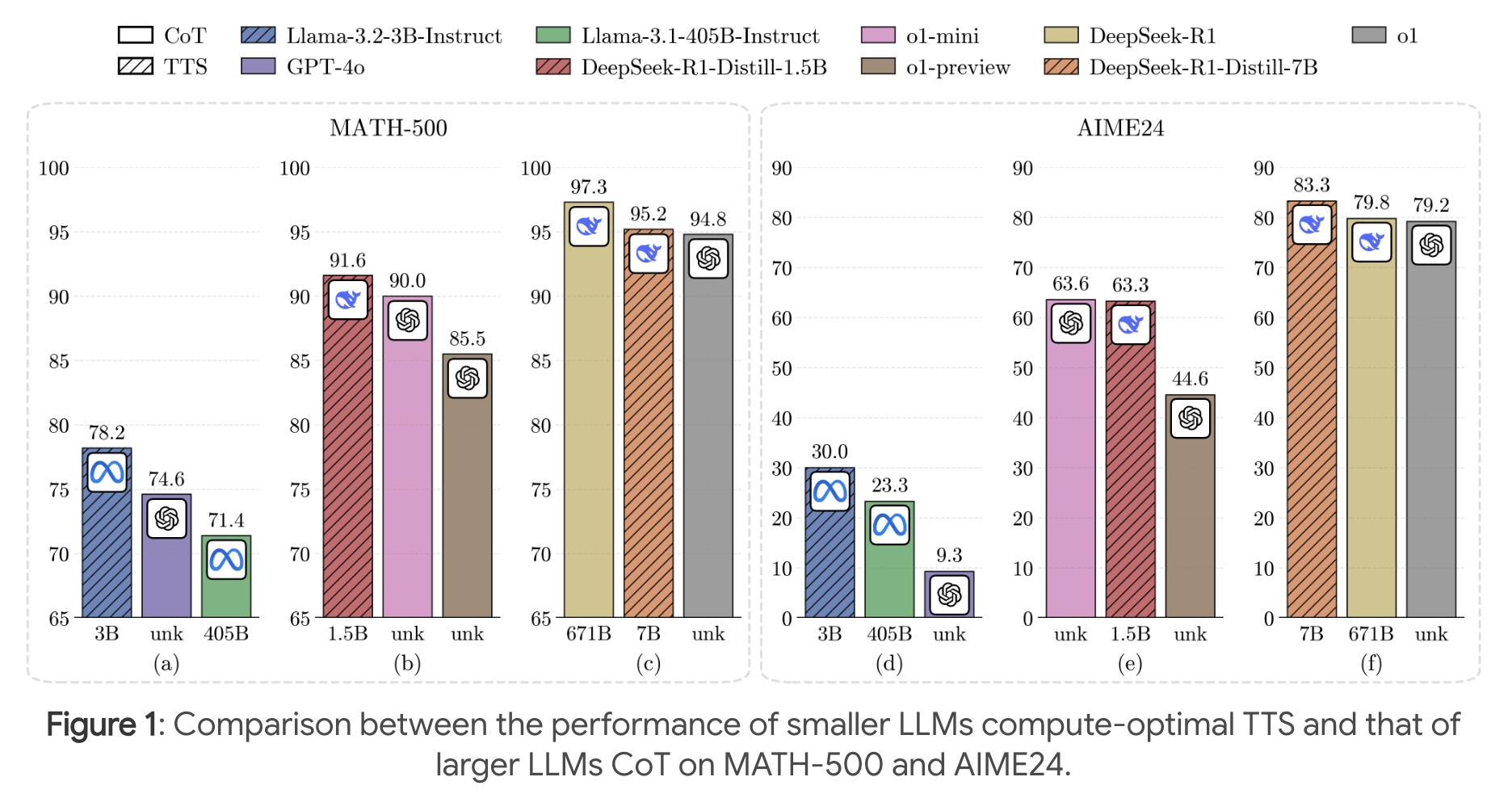
오늘은 아주 흥미로운 주제를 다룬 논문들[1] [2]을 소개하려 합니다. 바로 모델 크기를 키우는 대신, 추론 시간(Test-Time)에 더 많은 계산(Scaling)을 하는 방법을 제안한 논문입니다. 이 논문은 다양한 TTS(Test-Time Scaling) 기법에 대한 실험과 분석을 통해, 추론(reasoning)을 하는 과정에서 더 다양한 경로를 탐색함으로써 기존보다 훨씬 효율적으로 성능을 향상시킬 수 있음을 보여줍니다. 논문에 따르면, 적절한 TTS 전략을 사용하면 Llama 1B 모델이 동일 시리즈의 70B 모델보다 더 성능이 뛰어납니다. 심지어, deepseek 7B 모델이 동일 시리즈의 671B 모델을 뛰어넘고 1.5B 모델은 ChatGPT의 성능을 뛰어넘습니다!

image.png

Test-Time Scaling이란?

TTS는 LLM이 마치 어려운 문제를 푸는 사람처럼 추론 시점에 더 오래, 더 깊이 생각할 수 있도록 만드는 방법입니다. 일반적으로 LLM은 단 한 번의 forward pass로 응답을 생성하지만, TTS는 이 과정을 반복하여 다양한 응답을 탐색함으로써 최종 출력을 개선합니다. 여기서 중요한 것은 다른 decoding strategy 처럼 다음 단어를 반복 sampling 하는게 아니라, 추론(reasoning) 스텝을 반복하며 최적의 추론 경로를 찾아가는 것입니다!

Internal TTS VS External TTS

추론과정을 반복하기 위해서는 Internal TTS와 External TTS로 구분되는데 Internal TTS는 내부적으로 생각을 계속해서 할 수 있도록 강화학습을 추가하거나, 생성한 문장을 다시 revision할 수 있도록 fine-tuning이 필요합니다. 반면, External TTS는 verifier를 통해 중간 추론 과정을 평가하면서 더 나은 path를 찾아갑니다. Verifier는 [4] 논문에서 제안한 PRM(Process-supervised Reward Model)을 사용합니다. 여기서는 추가학습 데이터와 비용을 고려하여 External TTS만 고려합니다.

Reasoning Path Search Algorithm

TTS 알고리즘은 크게 다음 세 가지로 구분할 수 있습니다.

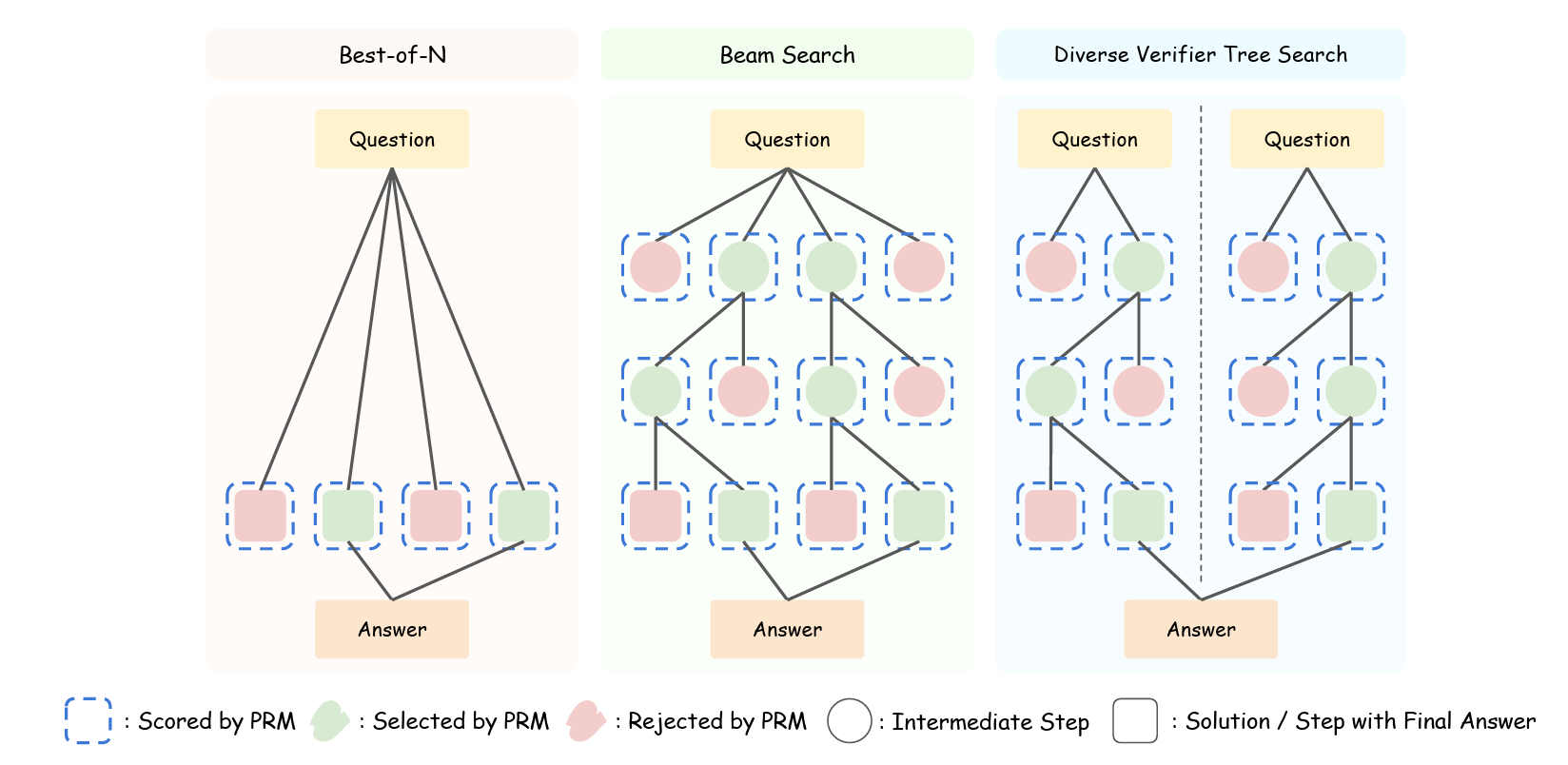
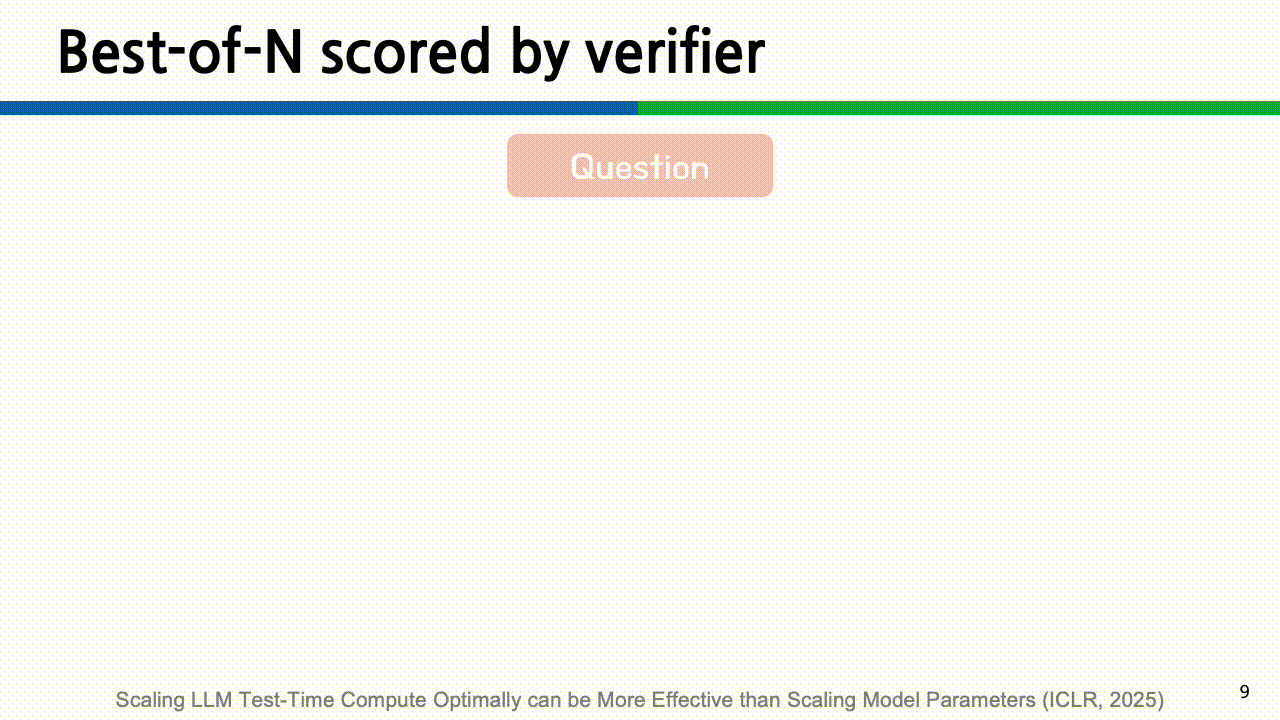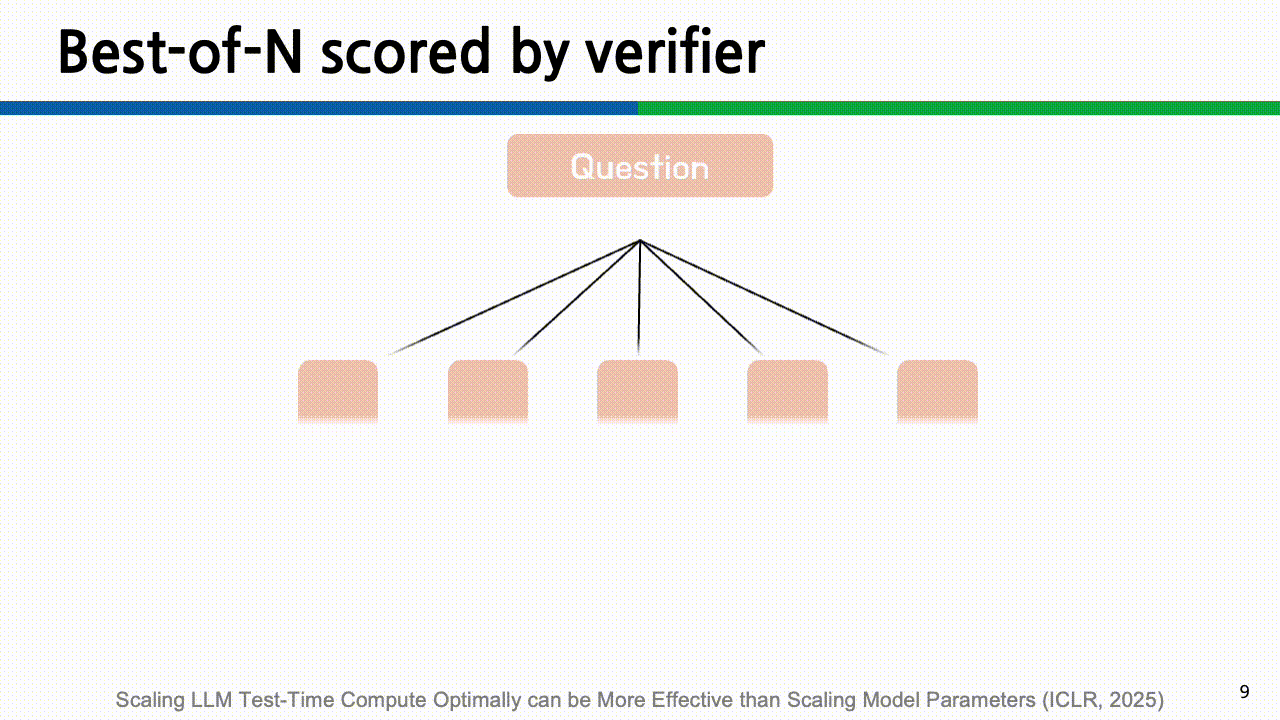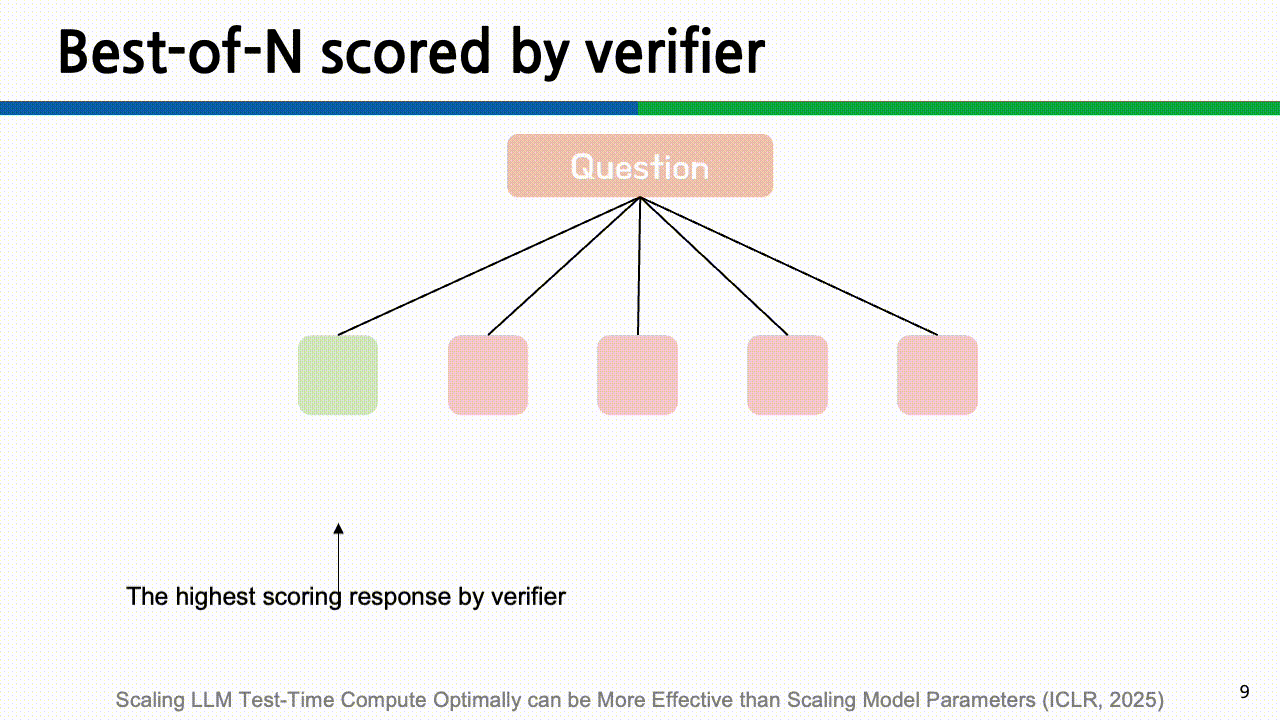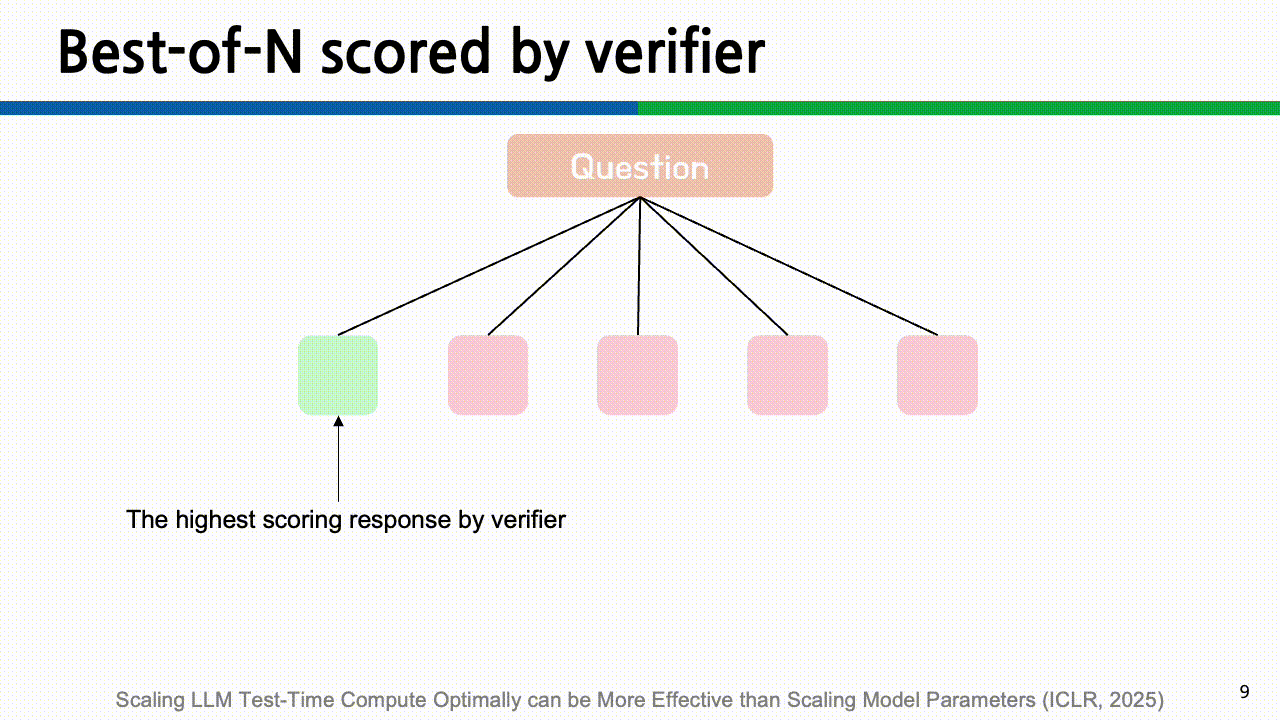
alt text

  1. BoN (Best-of-N): 가장 단순한 방식으로, 동일한 입력에 대해 N개의 응답을 샘플링한 후, 사전에 정의된 스코어링 기준에 따라 가장 우수한 하나를 선택합니다. Verifier를 사용하지 않고 단순히 출력에 대해 다수결(Majority Voting)로 결정하는것이 Naive BoN입니다. alt text 그리고 중간과정에 대한 평가를 하면서 tree를 탐색하지는 않지만, 최종 결과에 대해 추론 과정과 함께 verifier로 평가하여 가장 큰 값을 가진 결과를 찾는 방법이 논문에서 말하는 BoN입니다. alt text

  2. Beam Search: 단어 단위로 여러 후보 시퀀스를 동시에 확장해 나가는 decoding 전략과 이름이 똑같지만, 다른 알고리즘 입니다. BoN이 완성된 응답을 비교하는 방식이라면, Beam Search는 중간 과정 step을 평가하여 좋은 경로를 탐색해 나갑니다. 구체적으로 다음과 같은 과정을 거칩니다.
    1. beam width M 과 budget N 을 정합니다.
    2. N 만큼 추론과정을 샘플링 합니다.
    3. top-N/M 만큼 선택합니다.
    4. 뽑힌 노드에서 각각 M개 만큼 샘플링 합니다.
    5. 3~4 과정을 반복합니다. 이로써 항상 N개의 budget을 유지합니다.

    alt text

  3. Diverse Verifier Tree Search (DVTS): Beam Search를 확장한 형태로, 같은 문제에 대해 여러 Beam Search Tree를 만듭니다. 이를 통해 더 다양한 경로를 탐색합니다. [5]

    alt text

Compute-Optimal TTS 최적화 수식

[1]에서는 다음 수식을 제시하며, 테스트 시점에서 주어진 계산 Budget 하에 최적의 전략(strategy) $ \theta $ 를 찾는 문제를 정의했습니다.

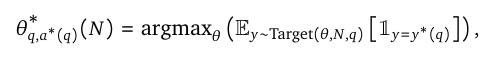
alt text

  • $ q $: 입력 질문
  • $ y^*(q) $: 정답
  • $ \text{Target}(\theta,N,x) $: 모델의 출력분포
  • $ \theta $: TTS 전략의 전략 (예: BoN, Beam Search, DVTS)
  • $ N $: 할당된 계산량, Budget (e.g. generation 횟수, beam width, FLOPs 등)

여기서 프롬프트의 난이도를 기준으로 최적의 TTS 전략을 선택하기 위해, 프롬프트를 5개의 difficulty bin으로 나누어 실험합니다. 각 난이도 수준별로 가장 성능이 좋은 전략과 하이퍼파라미터 조합을 사전에 계산해둡니다. 난이도는 base LLM이 해당 프롬프트에 대해 정답을 맞출 확률인 pass@1 rate를 기준으로 정의되며, 실제 테스트 시에는 주어진 프롬프트에 대해 2048개의 응답을 샘플링한 뒤, PRM을 활용해 각 응답의 정답 확률을 평가하고 이를 기반으로 프롬프트의 난이도를 추정합니다.

이와 유사하게 [2]에서는 위 수식에 reward model $ \mathcal{R} $을 추가하여 reward model까지 고려하여 최적 전략을 탐색합니다.

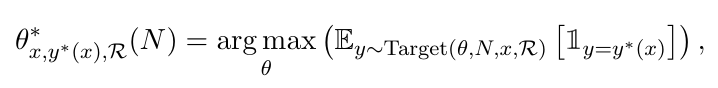
alt text

[2]에서는 결과값이 사용하는 모델과 PRM에 따라 큰 차이를 보이는 것으로 나타났습니다. 이에 따라 최적화 수식에서도 보상모델 $ \mathcal{R} $ 의 영향을 명시적으로 반영할 수 있도록 수식을 수정했습니다. 또한, 기존 연구보다 다양한 LLM과 PRM 조합에 대해 비교 실험을 수행하여, 각 난이도 구간에서 어떤 전략이 가장 효과적인지를 정량적으로 분석했습니다. 이러한 실험을 바탕으로 최적화 수식에 대응하는 최적의 전략 구성을 다음과 같이 찾을 수 있었습니다.

  • MATH-500
모델 크기 TTS 전략
< 7B Beam Search
7B ~ 32B DVTS (쉬움/중간) + Beam Search (어려움)
≥ 32B Best-of-N (BoN)
  • AIME24
모델 크기 TTS 전략
< 14B DVTS
≥ 14B Best-of-N (BoN)

실험 결과

Frontier 모델과 비교

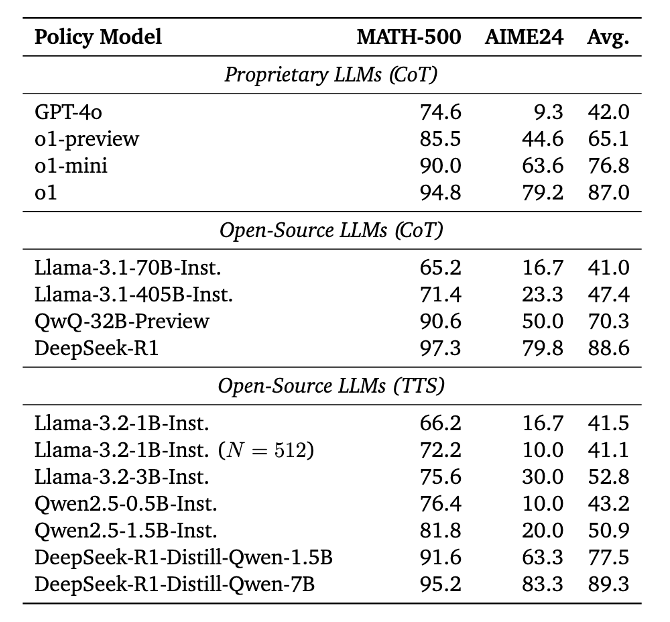
alt text

TTS를 적용한 소형 모델(SLM)들이 기존의 초거대 모델들을 능가하는 인상적인 결과를 보여줍니다. 대표적으로, TTS를 적용한 Llama3.2-3B 모델은 Llama3.1-405B 모델보다 높은 성능을 기록하며, 무려 135배나 작은 모델이 성능에서 앞서는 모습을 보였습니다. 특히 Budget N = 512 기준으로는 Llama3.2-1B 모델조차도 Llama3.1-405B를 MATH-500 벤치마크에서 능가하는 결과를 보였습니다. 또한, Qwen2.5-0.5B와 Llama3.2-3B 모델은 GPT-4o보다도 높은 성능을 기록했고, DeepSeek-Distill-1.5B는 OpenAI의 o1-mini를 능가하는 수준에 도달했습니다. 더불어 DeepSeek-Distill-7B 모델은 전체 비교 모델 중 최고 성능을 기록하며 TTS 전략의 효과를 극적으로 입증했습니다.

FLOPS 비교

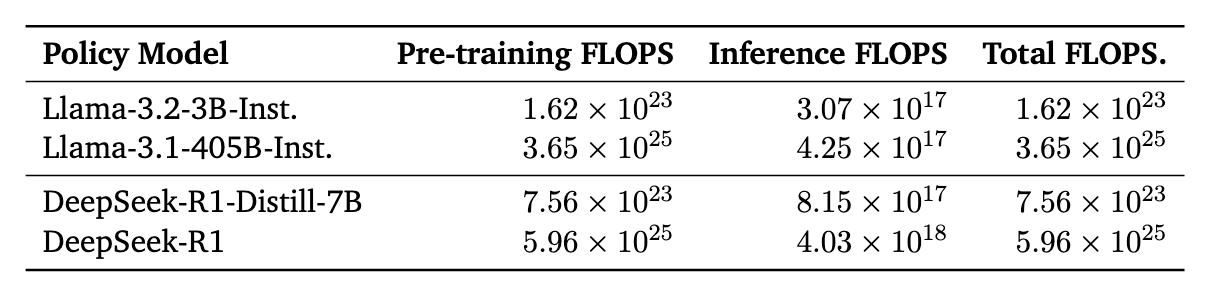
alt text

TTS를 적용한 모델의 FLOPS는 Budget에 따라 훨씬 더 많이 추론을 함에도 불구하고(e.g. N=512), 동일 시리즈의 가장 큰 모델에 비해 약 100~1000배 정도 적게 사용함을 볼 수 있습니다.

Long CoT와 비교

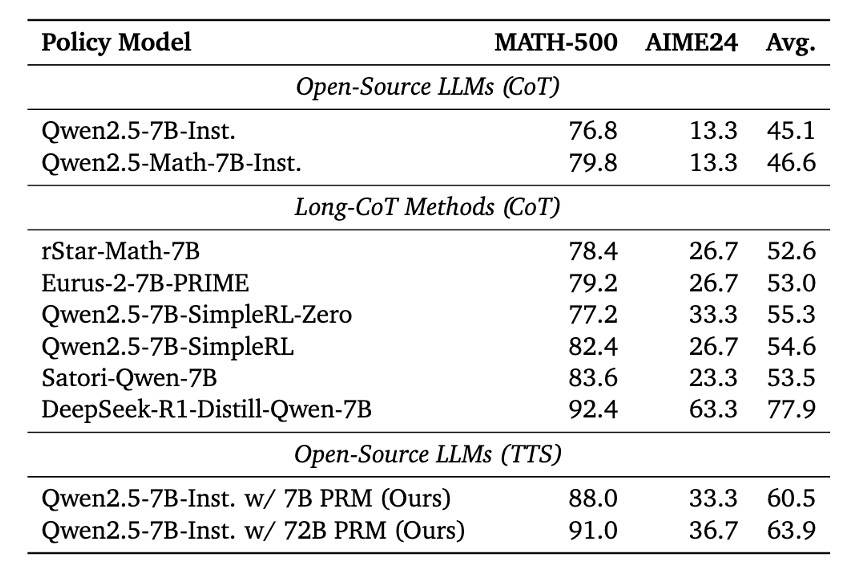
alt text

TTS를 적용한 Qwen2.5-7B 모델은 다양한 Long-CoT 기반 최신 방법들과 비교해서도 더 우수한 성능을 기록했습니다. 특히 rStar, Eurus-2, SimpleRL, Satori와 같은 방법들은 각각 강화학습, 온라인 학습, self-reflection, 또는 대규모 distillation 기법을 활용해 추론 능력을 향상시키지만, 그럼에도 불구하고 TTS 기반 Qwen2.5-7B는 MATH-500과 AIME24 양쪽 모두에서 평균 성능이 더 높게 나타났습니다.

한계점 및 마무리

이번 시간에는 소형 LLM(SLM)에 Test-Time Scaling 전략을 적용하여 초거대 모델보다 뛰어난 성능을 달성한 연구를 살펴보았습니다. 처음 논문을 접했을 때는 성능이 너무 극적이라 놀라움을 감출 수 없었지만, 실제로 코드를 실행해보고 내용을 차근차근 분석하면서 현재 이 방법이 가지는 분명한 한계점들도 확인할 수 있었습니다.

  1. 우선 PRM에 대한 의존도가 매우 큽니다. TTS의 성능은 PRM의 정확도에 크게 좌우되며, PRM 자체도 LLM을 파인튜닝한 모델이기 때문에 상당한 연산 자원과 비용이 필요합니다. 즉, TTS는 또 다른 고비용 모델이 필요하다는 점에서 근본적인 한계를 가집니다.
  2. 위 문제에서 파생된 제한점으로, 현재 TTS는 PRM이 잘 작동하는 수학 및 코딩 벤치마크에서만 성능을 보장할 수 있습니다. PRM을 학습하려면 각 추론 경로에 대해 정답 여부를 판단할 수 있어야 하는데, open-domain QA나 주관식 질문과 같은 일반적인 문제에서는 이러한 라벨링 자체가 매우 어렵습니다. 따라서 활용 범위가 아직 제한적입니다.
  3. TTS 전략 선택 최적화 수식은 이론적으로는 최적화 수식에 기반하지만, 실제 구현은 다양한 LLM과 PRM 조합을 미리 실험하여 그 결과를 하드코딩한 것에 가깝습니다. 향후 PRM의 구조나 학습 방식, 혹은 평가 기준이 바뀔 경우 지금의 최적 전략은 얼마든지 달라질 수 있습니다.

그럼에도 불구하고, 이 연구는 단순히 모델 크기나 학습 데이터에만 의존하지 않고, 추론 전략의 설계만으로도 성능을 획기적으로 향상시킬 수 있음을 보여주는 중요한 사례라고 생각합니다. 앞으로 PRM의 경량화, 다양한 문제 유형에 대한 일반화, 자동화된 전략 선택 등이 발전한다면, 소형 모델만으로도 실용적인 수준의 다양한 작업을 처리할 수 있는 시대가 머지않아 올 것이라 기대됩니다.

오늘도 읽어주셔서 감사합니다. 다음에 더 좋은 글로 찾아오겠습니다. 🤗

참고자료